Processo di carica e scarica di un condensatore in un circuito RC

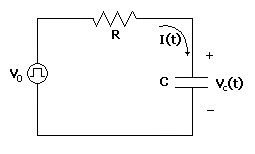
Il condensatore è un componente elettrico formato da due armature conduttrici separate da materiale isolante chiamato dielettrico che impedisce perciò il passaggio di corrente elettrica.
Quando il condensatore è inserito in un circuito RC contenente un generatore di differenza di potenziale, le cariche elettriche tendono a fluire da un polo all’altro del generatore attraversando la resistenza R e il condensatore C. Quest’ultimo carica le sue armature fino a che raggiungono una differenza di potenziale V_C uguale a quella del generatore V₀, cioè quando hanno accumulato una carica q=CV₀ e quando l’intensità diventa i=0. Dove V₀ è la forza elettromotrice del generatore e C è la capacità elettrica del condensatore.
Tra la chiusura del circuito e il raggiungimento dello stato di carica del condensatore, la carica elettrica presente sulle armature del condensatore e l’intensità i della corrente che passa attraverso la resistenza sono funzioni del tempo. Perciò V_R(t) e V_C(t) sono le d.d.p. ai capi della resistenza e del condensatore in un generico istante t. Poiché secondo la seconda legge di Kirchhoff V_R(t)+V_C(t)=V₀ , V_R(t)=R i(t) e V_C(t)=q(t)/C, si può scrivere:

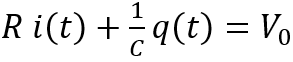
Sapendo che i=dq/dt l’equazione diventa:

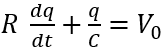
Questa equazione descrive il processo di carica del condensatore in funzione del tempo.
La soluzione q(t) di questa equazione differenziale di 1° ordine è:

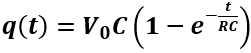
Quindi all’istante t=0, anche la carica del condensatore sarà 0, infatti q(0) = V₀C (1 – e^-0)=0, mentre per t → ∞ si avrà la carica massima ovvero q(∞)=V₀C(1 – e^-∞) =V₀C
Quando il condensatore è totalmente carico la V_C = V₀ e quindi q_max = V₀C

Poiché V_C(t)= q(t)/C, la differenza di potenziale tra le armature varia con la legge:

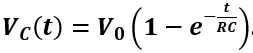
Si vede che all’inizio del processo di carica (t = 0) si ha: V_C(0)=V₀(1-e^-0)=0. Quindi all’istante iniziale il potenziale tra le armature sarà 0, mentre alla fine della carica di C (t  → ∞) si ha: V_C(∞)=V₀(1-e^–∞)=V₀ .

L’intensità di corrente nel circuito i(t)= dq/dt è data invece da:

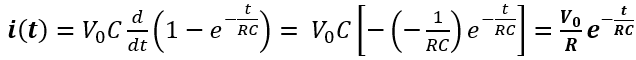
Si vede che la corrente è massima all’inizio della carica (t = 0), quando C è scarico: i(0) = V₀/R
Alla fine del processo di carica, (t → ∞), si ha: i = 0

La differenza di potenziale V_R(t) sulla resistenza R si ottiene dalla legge di Ohm (V_R = iR):

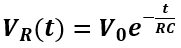
Quindi V_R decresce col tempo, partendo a t=0 V_R(0)=V₀e⁰ = V₀ fino al valore t → ∞   V_R (∞)=V₀e^-∞=0 , quando il condensatore sarà completamente caricato.

Per la carica di un condensatore molto importante è individuare la costante di tempo capacitativa τ (τ =RC).
Il significato fisico di τ si ottiene ponendo nell’equazione di carica t=τ, perciò:

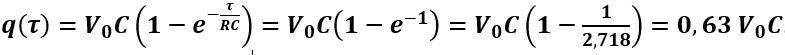
Quindi dopo un tempo t=τ la carica del condensatore arriva al 63% del valore finale V₀C. Maggiore è τ, più lenta è la carica del condensatore.

Per t=τ, invece, la V_C raggiunge il 63% del suo valore massimo V₀. Quindi, maggiore è τ, più lentamente cresce la V_C.

Analogamente, dopo un tempo t = τ, la corrente nel circuito RC in serie si è ridotta al 37% del suo valore massimo V₀/R.

Scarica di un condensatore

Quando il condensatore C è carico e la sua differenza di potenziale è V_C = V₀, collegando il condensatore parallelamente alla resistenza R, la carica q=V₀C presente sul condensatore fluisce attraverso R finché C si scarica completamente. Nel processo di scarica, la corrente attraversa la R in senso inverso rispetto alla carica di C.
Con V₀=0 la II legge di Kirchhoff diventa: V_R + V_C = 0. Dove V_R(t)=R i(t) e V_C(t)=q(t)/C e quindi:

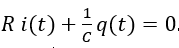
Sapendo che i=dq/dt l’equazione diventa:

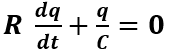
Questa equazione descrive il processo di scarica del condensatore in funzione del tempo.
La soluzione q(t) di questa equazione differenziale di 1° ordine è:

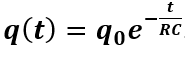
Dove q₀ è la carica iniziale del condensatore. Infatti per t=0, q=q₀ mentre per t → ∞, q=0. Per t=τ, q=0,37q₀
Quindi, quanto maggiore è τ, tanto più lentamente si scarica il condensatore.

Considerando la differenza di potenziale V_C, all’inizio della scarica è uguale a V₀ e decresce con il diminuire di q sulle armature fino a diventare 0 seguendo la legge esponenziale:

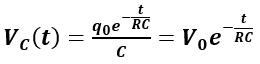
Si vede che all’inizio del processo di scarica (t = 0) si ha: V_C(0)=V₀e^-0=V₀, mentre alla fine della scarica di C (t → ∞) si ha: V_C(∞)=V₀e^–∞=0.
Per (t = τ): V_C(τ) =0,37V₀

Per quanto riguarda l’andamento della corrente durante il processo di scarica è:

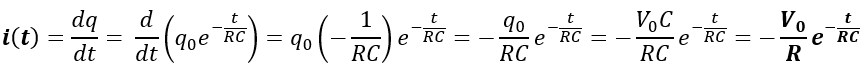
Il segno negativo indica che la corrente durante la scarica di C scorre in senso opposto rispetto al processo di carica.
Quando t=0, i= -V₀/R. Quando t → ∞, i=0
Quindi la corrente è massima all’inizio della scarica e decresce in maniera esponenziale.
La costante di tempo τ = RC ha lo stesso significato visto nella carica di C. Cioè dopo un tempo τ = RC, la corrente è diventata il 37% di quella iniziale.
In pratica si ha che un condensatore si è quasi tutto caricato o scaricato dopo 3τ. Infatti, per t = 3τ si ha:

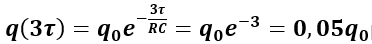
per il processo di scarica, mentre per il processo di carica si ha:

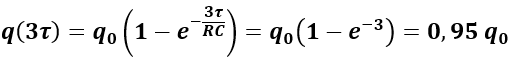
Fonte: Fisica biomedica.