OGGETTO: Determinazione della massa con una bilancia a bracci
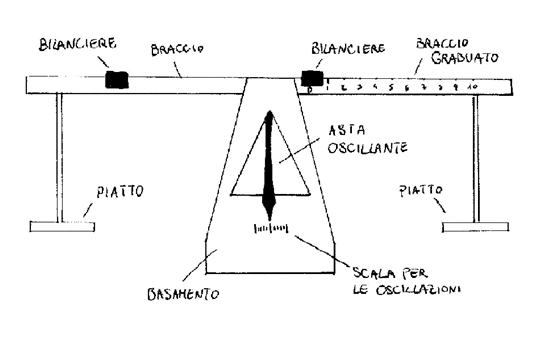
TABELLA:
| n° bancone | Massa della moneta in grammi [g] | Massa della moneta in grammi [g] (misurazione n°2) |
| 1 | 2.26 | 2.27 |
| 2 | 2.25 | 2.27 |
| 3 | 2.27 | 2.26 |
| 4 | 2.31 | 2.31 |
| 5 | 2.25 | 2.26 |
| 6 | 2.33 | 2.33 |
| 7 | 2.27 | 2.28 |
| 8 | 2.32 | 2.32 |
| 9 | 2.20 | 2.26 |
| 10 | 2.27 | 2.25 |
STRUMENTI E APPARECCHI:
- Bilancia a due bracci con relativi pesetti;
- 3 Monete da 1 centesimo.
RELAZIONE:
CONOSCENZE TEORICHE:
Un obiettivo delle esperienze è stato determinare la sensibilità della bilancia, cioè la più piccola misura che essa può apprezzare. La sensibilità di qualsiasi strumento di misurazione è, appunto, la precisione che esso può garantire. La sensibilità corrisponde all’errore assoluto (Ɛa), che ha le stesse misure fisiche della misurazione. Un comune righello, ad esempio, ha sensibilità 1mm e un Ɛa=1mm, perché possiamo leggere con sicurezza i centimetri, ma la cifra rappresentata dai millimetri è incerta, in quanto spesso non coincide esattamente con una tacca del righello stesso. Naturalmente, maggiore è la sensibilità, maggiore sarà l’accuratezza della misurazione.
La bilancia da me utilizzata si componeva di varie parti: un basamento in plastica, due braccia, due piatti dove appoggiare gli oggetti, un’asta oscillante collegata ai bracci, che quantifica l’ampiezza delle oscillazioni grazie ad una piccola scala graduata presente sul basamento. Grazie alla scala possiamo confrontare le oscillazioni a destra con quelle a sinistra, per vedere se i piatti sono in equilibrio. Fondamentali sono anche i due bilancieri, che consentono di tarare la bilancia stessa e, come si vedrà, di aumentare la sensibilità.
Per misurare dobbiamo attenerci ad un procedimento rigido, al fine di ottenere una misurazione la più veritiera possibile. Per prima cosa dobbiamo tarare la bilancia; in questo sono fondamentali i bilancieri. Uno dei due, che permette di misurare i centesimi di grammo (ed è proprio questa la sensibilità della bilancia) è posto sul braccio graduato, quello di destra. Dobbiamo spostarlo sullo zero. Quello di sinistra deve essere mosso osservando l’asta oscillante: quando questa segna sulla scala le stesse oscillazioni sia a destra sia a sinistra la bilancia è in equilibrio. L’operazione potrebbe richiedere un po’ di tempo, ma è indispensabile. È importante non spostare i due bilancieri, altrimenti si deve ricominciare tutta procedura. Dopodiché si può cominciare la misurazione. Si appoggia sul piatto di sinistra l’oggetto considerato e sul destro i pesetti in progressione, per determinare tra quali misure questo sia compreso. Se un peso fa scendere e inclinare le braccia si dovrà utilizzarne uno di massa minore.
La scala graduata del braccio destro è divisa in intervalli regolari: questi rappresentano 0.01 g ognuno.
Quindi, quando abbiamo utilizzato i pesi e ci siamo avvicinati alla misura reale, spostiamo il bilanciere di destra in corrispondenza di ogni tacca, finché troviamo quella che fa mantenere le stesse oscillazioni a destra e a sinistra sulla scala sul basamento della bilancia. In questo modo determiniamo due cifre decimali, di cui la seconda è quella incerta. Abbiamo così ottenuto la misurazione, con un errore assoluto Ɛa=0.01 g.
Esempio: con i pesi la misurazione si avvicina a 1,5 g, perché la bilancia si avvicina all’equilibrio con 1 peso da 1 g e con uno da 500 mg. Per determinare i centesimi di grammo sposto il bilanciere di destra su un numero, ad esempio 5, e osservo che l’asta oscillante indica le stesse oscillazioni sul basamento: ho raggiunto l’equilibrio. La mia misurazione sarà quindi 1 + 0.5+ 0.05 = (1.55±0.01) g.
DESCRIZIONE DELLA PROVA:
Per prima cosa abbiamo tarato la bilancia e abbiamo verificato la sensibilità. Sul piatto di sinistra ho appoggiato un peso da 100 mg (=0.01 g) e ho spostato il bilanciere di destra sul 10. La bilancia era in equilibrio, quindi se 100 mg a sinistra sono in equilibrio con solo il bilanciere sul 10 a destra, 10=100 mg, cioè ogni tacca misura 0.01 grammi.
Dopo questa verifica ho misurato tre monete da un centesimo di euro, di cui una scambiata con un compagno.
La prima moneta pesata ha dato massa: (2.30±0.01) g. Tutte le misurazioni della classe hanno dato lo stesso esito.
La seconda ha dato un risultato leggermente diverso e, in particolare, la classe ha rilevato che la moneta che ognuno di noi aveva a disposizione differiva nella massa dalle altre.
La misurazione n°1 e la n°2 hanno dato masse simili. La grandezza più veritiera è da ricercarsi nella media matematica dei risultati ottenuti. Questo risultato può essere migliorato eseguendo molte misurazioni.
Tuttavia bisogna tenere conto della sensibilità dello strumento, che, per quanto accurato possa essere, è affetto sempre da un margine di errore più o meno consistente.
La misurazione effettuata si compone, nel nostro caso, di due cifre certe (la parte intera e il primo decimale) e di una incerta, che coincide con la sensibilità dello strumento.
CONCLUSIONI:
Grazie alle foto, alle tabelle e alle osservazioni ho illustrato come utilizzare la bilancia a due braccia per ottenere una misurazione precisa sfruttando al massimo la sensibilità dello strumento.



