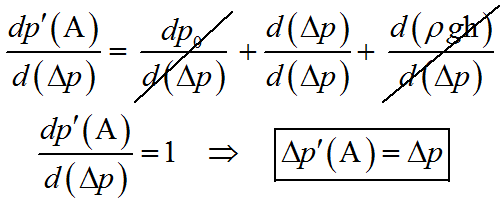La statica dei Fluidi – Da Stevino ad Archimede

In questo articolo tratteremo la statica dei fluidi. Un fluido è una sostanza che si deforma illimitatamente se sottoposto ad uno sforzo di taglio. Esso ha la capacità di scorrere e non ha una forma propria. I fluidi comprendono sia le sostanze liquide che quelle gassose, tuttavia ci sono dei fluidi particolari costituiti da catrame e gomma.
Siccome i fluidi non hanno una forma propria e quindi un volume ben definito, è obbligatorio introdurre una nuova grandezza di misura: la densità di massa, ovvero la massa dell’unità di volume.

ρ = m/V

Questa grandezza si misura in kg/m³ nel sistema internazionale e gr/cm³ nel sistema di Gauss. Ogni sostanza ha una sua densità.

Un’altra grandezza utile ai fini della statica dei fluidi è il peso specifico: il peso dell’unità di volume.

γ = P/V = m⋅g/V = ρ⋅g

Questa grandezza si misura in N/m³ nel sistema internazionale e dyne/cm³ nel sistema di Gauss.

La Pressione

Quando si applica una forza su una superficie piana di un fluido nasce una nuova grandezza fisica: la pressione.

p = F_⊥/S

Dove F_⊥ è la componente perpendicolare della Forza (F) sulla superficie (S).
Se un fluido è contenuto in un recipiente, la pressione esercitata sulle pareti si può evidenziare sperimentalmente con una membrana elastica che si deforma, indicando l’azione di una forza esercitata perpendicolare ad essa.
La pressione p ad una determinata profondità h di un fluido in quiete ha lo stesso valore in ogni direzione. Se non fosse così, il fluido sarebbe in movimento.
La mancanza di proprietà direzionali fa si che la pressione sia una grandezza scalare le cui unità di misura sono il N/m² o Pascal (Pa) nel sistema internazionale e il dyne/cm² o Baria (Ba) nel sistema di Gauss. 1 Pascal corrisponde a 10 Barie.
Altre unità di misura della pressione sono l’atmosfera (atm) che indica la pressione media dell’atmosfera al livello del mare: 1 atm = 760 mm Hg = 760 torr = 1 bar.
La pressione atmosferica è equivalente a quella di una colonna di mercurio alta 760 mm che a sua volta corrisponde a 1,01⋅10⁵ Pa.

Legge di Stevino (pressione idrostatica)

Si sa che quando si scende in profondità di un liquido la pressione aumenta, mentre diminuisce con l’altezza quando si sale in montagna.
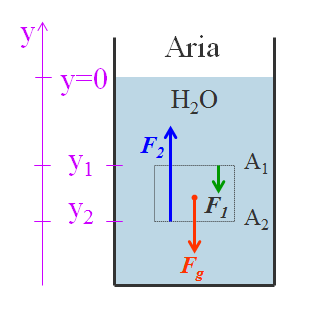
Per poter calcolare questo aumento o diminuzione di pressione bisogna considerare un fluido in equilibrio. Quindi immaginiamo un ipotetico cilindro immerso e ripieno di un liquido con base A e poniamo y₁ e y₂ come profondità delle due basi del cilindro. Il campione di liquido nel cilindro si trova in equilibrio statico in quanto su di esso agiscono tre forze:

1. La forza peso F_g = m⋅g;
2. La forza F₁ sulla faccia superiore A₁ dovuta alla pressione del liquido su A₁;
3. La forza F₂ sulla faccia inferiore A₂ che deve bilanciare F₁ + F_g perché il cilindro è in equilibrio statico;

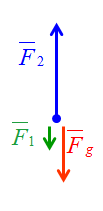
Proprio perché il cilindro è in equilibrio statico, la somma di queste tre forze deve essere uguale a 0:

F_g + F₁ + F₂ = 0 quindi F₂ = F₁ + m⋅g

Se consideriamo p₁ la pressione in profondità y₁, ovvero F₁ = p₁⋅A₁, e p₂ la pressione in profondità y₂, ovvero F₂ = p₂⋅A₂.
Se m è la massa di liquido nel cilindro allora: m = ρ⋅V = ρ⋅A₁⋅(y₁-y₂)
Se adesso sostituiamo la massa con le pressioni p₂⋅A₂ = p₁⋅A₁ + ρ⋅A₁⋅(y₁-y₂)⋅g

Alla fine rimane la relazione: p₂ = p₁ + ρ⋅g⋅(y₁-y₂)

Questa relazione vale sia per i liquidi (in funzione della profondità) sia per l’atmosfera (in funzione dell’altitudine).

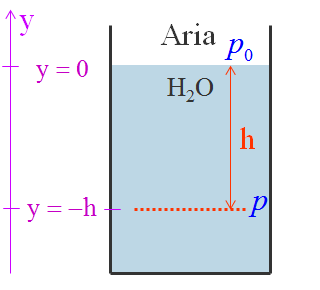
Se adesso poniamo y₁ = 0 ; p₁ = p₀ ; y₂ = -h ; p₂ = p otteniamo la legge di Stevino:

p = p₀ + ρ⋅g⋅h

Dalla legge di Stevino si può comprendere come la pressione presente in un punto di un fluido in equilibrio statico, dipende solo dalla profondità di quel punto e non dalla posizione in orizzontale o dalla forma del contenitore.
In generale la p si chiama pressione assoluta, mentre ρ⋅g⋅h si chiama pressione relativa e rappresenta il peso di colonna di un fluido su una superficie unitaria.

Misura della pressione (Esperienza di Torricelli)

Tra i fluidi che esercitano una pressione c’è anche l’aria. Questa pressione prende il nome di pressione atmosferica e agisce su tutti i corpi immersi nell’aria. Tale pressione venne misurata per la prima volta da Torricelli con il barometro a mercurio inventato da lui stesso. (leggi questo articolo per capire l’esperimento)
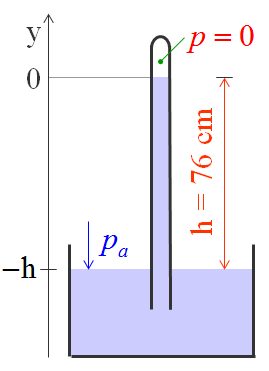
Se applichiamo la legge di Stevino a profondità y₂ = -h, in questo caso in cui p_a è la pressione atmosferica che agisce sulla superficie del mercurio ed è anche la pressione a profondità y = -h nel tubo verticale dato che p = 0 nella parte vuota del tubo (trascurando la tensione di vapore del mercurio a 20 °C), allora:

p(y₂ = -h) = p₀(y = 0) + ρ_Hg⋅g⋅h quindi:
p_a = 0 + ρ_Hg⋅g⋅h ovvero p_a = ρ_Hg⋅g⋅h

La pressione atmosferica è equivalente alla pressione esercitata dalla colonnina di mercurio alta 76 cm a 0 °C e con g = 9,81 m/s². Questa pressione è uguale al peso della colonna di mercurio di sezione unitaria misurata al livello del mare. Se cambia la pressione atmosferica, cambia anche l’altezza h della colonna di Hg.

Il principio di Pascal

Secondo il principio di Pascal del 1652, se un fluido è in equilibrio statico e su di esso si varia la pressione esterna p₀ di una quantità Δp, questa variazione si trasmette, istantaneamente ed inalterata, in ogni punto del fluido e sulle pareti del recipiente che lo contiene.
Si consideri un fluido di densità ρ contenuto in un recipiente su cui è applicata una pressione esterna p₀. La pressione p nel generico punto A è:

p(A) = p₀ + ρ⋅g⋅h

Se si varia la pressione esterna p₀ di Δp, la nuova pressione p'(A) nel punto A sarà:

p'(A) = p₀ + Δp + ρ⋅g⋅h

Il principio di Pascal può essere dimostrato derivando p'(A) rispetto a Δp supponendo che il fluido sia un liquido incomprimibile (ρ = costante):

Essendo A un punto generico, la variazione di pressione è la stessa in ogni punto del liquido.
Un esempio in cui si applica il principio di Pascal lo si ha quando si preme il fondo di un tubo di dentifricio: il contenuto fuoriesce dall’apertura perché l’aumento di pressione sull’involucro si trasmette istantaneamente in ogni punto del tubo.

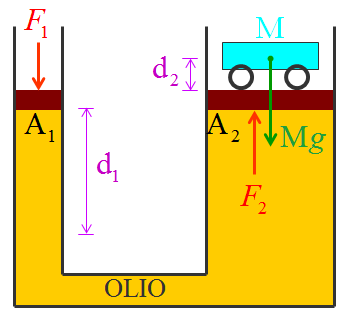
Un’altra applicazione importante del principio di Pascal è la leva idraulica, usata per sollevare oggetti pesanti.
Per sollevare un carrello di peso M⋅g occorre una forza F₂ esercitata dalla pressione del fluido sul pistone A₂ che sia uguale e contraria: F₂ = M⋅g.
Se si applica una forza F₁ sul pistone di A₁, esercitando una pressione p = F₁/A₁, essa viene trasmessa attraverso il fluido fino al pistone A₂, quindi:

p = F₁/A₁ = F₂/A₂  quindi la F₁ necessaria è F₁= F₂⋅(A₁/A₂).

Sapendo che F₂ = M⋅g allora F₁= M⋅g⋅(A₁/A₂).

Da questa relazione si può benissimo capire che se l’area del secondo pistone è superiore a quella del primo pistone, allora occorrerà una forza minore per sollevare il carrello.
I freni idraulici e gli elevatori idraulici utilizzano questo principio.

Il Principio di Archimede

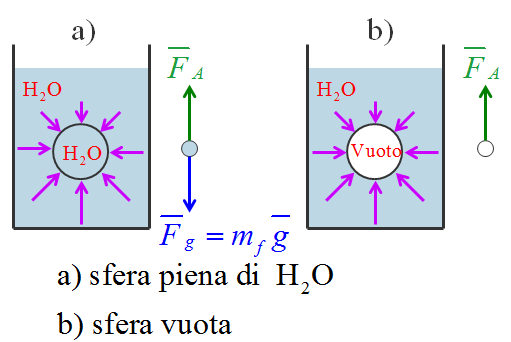
Si consideri un guscio sferico di massa trascurabile all’interno di un recipiente pieno di liquido in condizioni statiche.

Nel caso a), la sfera è in equilibrio statico in quanto la forza peso F_g è bilanciata da una forza verso l’alto F_A dovuta al fluido circostante tale che F_g + F_A = 0.
La spinta F_A che agisce dal basso e consente il galleggiamento si chiama spinta di Archimede. Questa spinta è una conseguenza della legge di Stevino, infatti, la pressione cresce con la profondità e la pressione nella parte inferiore della sfera è maggiore della pressione sulla parte superiore.
La spinta di Archimede è la risultante delle forze di pressione che agiscono sulla sfera. In particolare, le componenti orizzontali di queste forze si elidono, a parità di profondità.

Nel caso b), invece, la sfera è vuota e la forza peso è uguale a 0 (F_g = 0), tuttavia la distribuzione delle forze di pressione sulla superficie della sfera rimane la stessa e la risultante di queste forze è sempre F_A.

Per poter calcolare la spinta di Archimede nel primo caso basta sapere che la sfera piena di acqua è in equilibrio statico quindi: F_g = F_A.
Se identifichiamo con m_l la massa di liquido nella sfera F_g = m_l⋅g quindi:

F_A = m_l⋅g = ρ_l⋅V⋅g

Qui la spinta di Archimede che si esercita sulla sfera è pari al peso dell’acqua in esso contenuta.

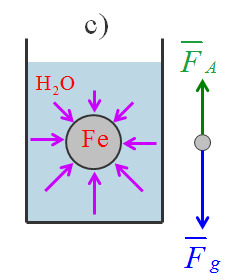
Se in un terzo caso c) prendessimo una sfera piena di ferro dello stesso volume, le forze che agirebbero sulla sfera sarebbero le stesse di quelle che avrebbero agito sulla sfera di acqua dato che il volume è rimasto identico. La sfera di ferro è soggetto alla stessa spinta di Archimede verso l’alto, ovvero sempre uguale al peso di H₂O spostata dalla sfera di ferro di volume V: F_A = ρ_H2O⋅V⋅g

Tuttavia, nel caso della pallina di ferro, per calcolare la forza peso bisogna considerare la densità del ferro: F_g = ρ_Fe⋅V⋅g. Essendo la densità del ferro maggiore della densità dell’acqua, si può capire come di conseguenza anche la forza peso è maggiore della forza di Archimede. Questa condizione porta alla sfera a non essere in equilibrio statico e perciò affonda con una spinta verso il basso pari a:

F = F_g – F_A = ρ_Fe⋅V⋅g – ρ_H2O⋅V⋅g = (ρ_Fe – ρ_H2O)⋅V⋅g

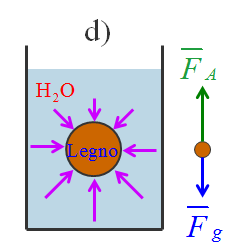
Se prendiamo come ultimo caso d) una sfera di legno dello stesso volume delle altre sfere, le forze di pressione che agiscono sulla sfera di legno sono le stesse che agivano sulla sfera di acqua e quella di ferro essendo il volume uguale. Quindi la sfera di legno è soggetta alla stessa spinta di Archimede verso l’alto.
In questo caso, però, la forza peso è calcolata considerando la densità del legno, che è di gran lunga inferiore a quella del ferro e dell’acqua, quindi anche la forza peso è inferiore alla spinta di Archimede. Le due forze sono diverse e anche in questo caso la sfera non è in equilibrio statico, ma è spinta verso l’alto con una forza pari a:

F = F_A – F_g = ρ_H2O⋅V⋅g – ρ_L⋅V⋅g = (ρ_H2O – ρ_L)⋅V⋅g

Il principio di Archimede sancisce quindi che un corpo immerso interamente o parzialmente in un fluido è soggetto ad una spinta verso l’alto, la cui intensità è pari al peso del fluido spostato dal corpo stesso.
La spinta di Archimede esercitata da un fluido su di un oggetto non dipende né dal materiale, né dalla forma dell’oggetto, ma solo dal volume di fluido spostato. A parità di volume di fluido spostato, oggetti diversi risentono della stessa spinta verso l’alto pari al peso del volume di fluido spostato.