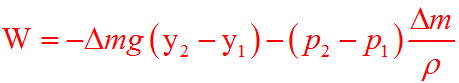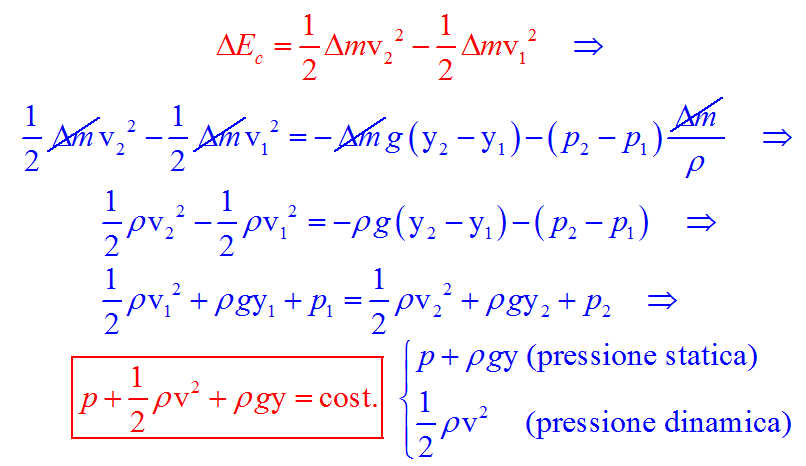Bernoulli, nel 1738, si preoccupò di applicare il principio di conservazione dell’energia nei fluidi.
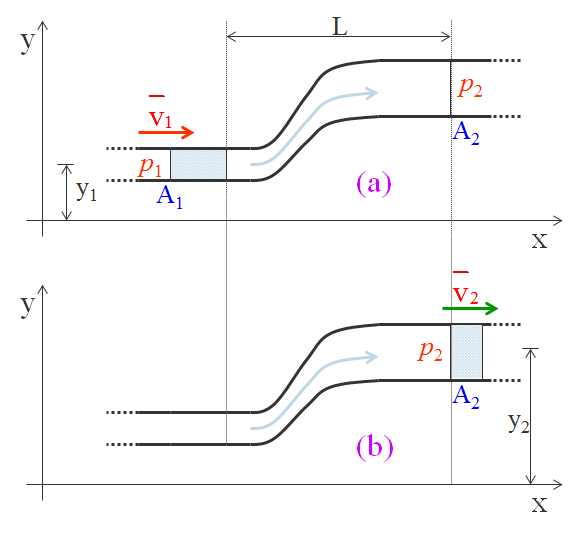
Per fare ciò, bisogna considerare un fluido ideale che scorre in un tubo in moto laminare. Il fluido è incomprimibile, ovvero la densità è costante, quindi in un intervallo di tempo Δt un volume di fluido ΔV attraversa la sezione A1 in entrata ed un identico volume ΔV fuoriesce dal tubo attraverso la sezione A2.
Il teorema di Bernoulli si dimostra applicando il principio di conservazione dell’energia meccanica del fluido che scorre nel tubo tra la configurazione iniziale a) e finale b) (si considera la parte di fluido tratteggiata in azzurro che si muove tra i due piani verticali separati dalla distanza L).
Il teorema dell’energia cinetica afferma che il lavoro è uguale alla variazione di energia cinetica: W = ΔEc
Per calcolare il lavoro bisogna considerare le forze che agiscono sul sistema, ovvero la forza di gravità e le forze di pressione.
Il lavoro Wg fatto dalla forza di gravità è uguale alla forza peso Δm⋅ḡ per la variazione di quota Δy:
Wg = Δm⋅ḡ⋅Δy = -Δm⋅g⋅(y2-y1)
Il lavoro esercitato dalla forza peso è negativo in quanto la forza è rivolta verso il basso, mentre lo spostamento è rivolto verso l’alto, formando insieme un angolo di 180° il cui coseno è -1. La Δm di massa considerata nel lavoro è quella relativa alla massa di fluido tratteggiata.
Il lavoro compiuto invece dalle forze di pressione è in parte compiuto sul sistema (all’ingresso A1) per spingere il fluido attraverso il tubo, ed in parte dal sistema (all’estremità di uscita A2) per spingere il fluido fuori dal tubo in presenza di p2.
Il lavoro di una forza di pressione p che agisce su una porzione di fluido contenuta in un tubo di sezione A per spostarla di una distanza Δx è, essendo A⋅Δx = ΔV:
F⋅Δx = (p⋅A)⋅(Δx)⋅cosθ = ±p⋅ΔV
Quindi il lavoro della p1 svolto sul sistema è: Wp1 = p1⋅ΔV
Mentre il lavoro della p2 svolto sul sistema è: Wp2 = -p2⋅ΔV
Come il lavoro svolto dalla forza di gravità, anche il lavoro svolto dalla pressione nel secondo punto è negativo in quanto la forza e lo spostamento hanno versi opposti. Alla fine di tutto, il lavoro delle pressioni sarà:
Wp = Wp1 + Wp2 = p1⋅ΔV – p2⋅ΔV = -(p2-p1)⋅ΔV
Il lavoro totale invece compiuto sulla massa Δm sarà:
W = Wg + Wp = -Δm⋅g⋅(y2-y1) – (p2-p1)⋅ΔV
Ricordando che la densità è la massa in un volume: Δm/ΔV = ρ e che quindi ΔV = Δm/ρ il lavoro è uguale a:
Se dal teorema dell’energia cinetica W = ΔEc sostituiamo la variazione dell’energia con le velocità e il lavoro con quello ricavato da noi precedentemente, quindi semplifichiamo le masse e moltiplichiamo i membri per la densità ρ:
Alla fine avremo la somma senza indici perché 1 e 2 si riferiscono a due punti qualsiasi del fluido. Questa somma rimane costante nel tempo se il fluido preso in considerazione è ideale (presenta quindi le caratteristiche di essere incomprimibile, non viscoso, irrotazionale e si muove di moto laminare).
Il teorema di Bernoulli, alla fine dei conti, non è una nuova legge, bensì un nuovo modo di esprimere la conservazione dell’energia meccanica nel caso dei fluidi.
Nella formula finale, la somma p+ρ⋅g⋅y ricorda in un certo senso la legge di Stevino e l’energia potenziale del fluido e si riguarda la pressione statica, mentre ½⋅ρ⋅v2 rappresenta l’energia cinetica del fluido e riguarda la pressione dinamica.
Questa nota finale sta a dimostrare come l’idrostatica è un caso particolare della dinamica dei fluidi. Infatti, la legge di Stevino è un caso particolare dell’equazione di Bernoulli, ovvero quando un fluido è in quiete e la velocità iniziale corrisponde con quella finale ed è uguale a 0.