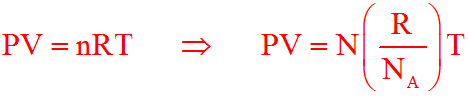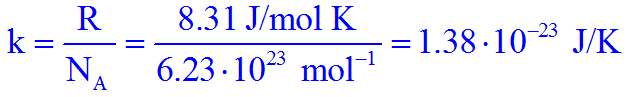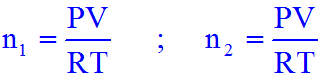I gas, poiché si espandono molto ed occupano sempre tutto il volume del contenitore, a differenza dei solidi e dei liquidi a pressione costante, non possono seguire l’espressione della dilatazione volumica: ΔV = V0⋅β⋅ΔT
Il volume di un gas dipende fortemente dalla pressione e dalla temperatura, oltre che dalla sua massa.
Le tre grandezze pressione (P), volume (V) e temperatura (T), sono storicamente legate a tre leggi sperimentali che sono uguali per tutti i gas in condizioni particolari: con bassa densità (con pressione non troppo alta) e in condizioni di alta temperatura rispetto alla temperatura di liquefazione.
La prima legge osservata è la legge di Boyle e Mariotte. Essa risale al diciassettesimo secolo e dice che a temperatura costante, il prodotto tra pressione e volume rimane costante.
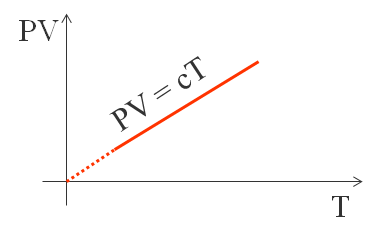
Sperimentalmente si osserva che il valore della costante, a parità di massa e con lo stesso tipo di gas, dipende dalla temperatura alla quale avviene la variazione di pressione e volume. Quindi il valore della pressione per il volume, per una certa massa di gas, è un indice della temperatura del gas stesso. Fisicamente si definisce la temperatura del gas come una grandezza proporzionale al prodotto P⋅V, ovvero: P⋅V = c⋅T
La costante c dipende dalla massa del gas e dal tipo di gas.
Si può usare la legge di Boyle per costruire un termometro con la scala assoluta e non utilizzando un modo arbitrario. A differenza dei termometri a scala arbitraria, come quello a mercurio, il termometro a gas (in genere usando l’elio) misura una temperatura che dipende proprio dallo stato fisico del gas, ovvero alla sua pressione e al suo volume a quella temperatura.
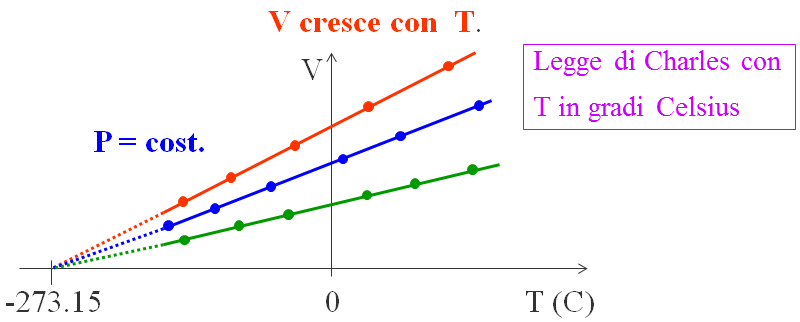
Fu il fisico francese Charles che, un secolo più tardi, formulò una seconda legge individuando che per un gas a pressione costante (la cui pressione non deve essere troppo alta, in modo che la distanza tra le molecole sia tale da poter trascurare le interazioni molecolari), estrapolando la retta che interpola i punti sperimentali, si ha che l’intercetta con l’asse orizzontale è per tutti i gas la temperatura di -273,15 °C. Per ogni gas Charles trovò una legge lineare, fino ad un certo punto, perché al di sotto di determinati valori il gas diventa liquido. Tuttavia, prolungando le rette (la zona tratteggiata), tutte si univano nel punto segnante -273,15 °C.
Questa temperatura è chiamata zero assoluto perché al di sotto di tale valore il gas non può esistere perché avrebbe un volume negativo, perciò è la più bassa temperatura possibile in natura. Molti esperimenti recenti confermano tale risultato.
Lo zero assoluto è proprio la base per la scala di temperatura assoluta o scala Kelvin.
La relazione lineare tra V e T della legge di Charles è: V = V0⋅(1+γ⋅ΔT).
Dove V0 è il volume del gas a 0 °C e ΔT è misurata rispetto a T = 0 °C.
Se la V = 0 allora V0⋅(V0⋅(1+γ⋅ΔT) e quindi 1+γ⋅ΔT = 0. Isolando la variazione di temperatura e poi sostituendola con il valore dello zero assoluto ci possiamo poi individuare γ:
ΔT = -1/γ = -273,15 °C e quindi: γ = 1/273,15 °C-1.
Questo significa che per tutti i gas molto rarefatti (a bassa pressione) e con temperature abbastanza alte rispetto alla temperatura di liquefazione, si ha lo stesso valore di γ = 1/273,15 °C-1 che è proprio uguale al coefficiente di dilatazione volumica β dell’aria e di molti altri gas a pressione atmosferica (β = 3,4 ⋅ 10-3 °C-1).
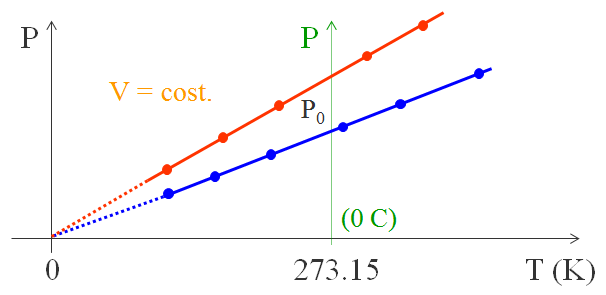
La seconda legge conosciuta è la legge di Gay-Lussac. In condizioni di gas rarefatto e con temperature abbastanza alte rispetto a quella di liquefazione, questo fisico inglese trovo che in un gas, mantenendo costante il volume, la sua pressione è direttamente proporzionale alla temperatura assoluta.
Un esempio pratico è rappresentato dalla bomboletta di spray che se messa a contatto con il fuoco esplode per l’aumento di pressione del gas al suo interno.
La relazione tra P e T è: P = P0⋅(1+γ⋅ΔT). Dove P0 è la pressione del gas a 0 °C e ΔT è misurata rispetto a T = 0 °C.
Qui valgono le stesse considerazioni della legge di Charles, infatti se la P = 0 allora P0⋅(1+γ⋅ΔT) = 0 e quindi 1+γ⋅ΔT = 0. Isolando la variazione di temperatura e poi sostituendola con il valore dello zero assoluto ci possiamo poi individuare γ:
ΔT = -1/γ = -273,15 °C e quindi: γ = 1/273,15 °C-1.
Dalle leggi dei gas è nata l’equazione di stato dei gas perfetti.
Nella legge di Boyle si era visto come, a temperatura costante, il prodotto tra P e V è costante in base alla massa del gas.
Infatti, gonfiando un pallone sappiamo che più aria vi entra, più grande diventa il pallone. In questo esempio, la pressione rimane costante (quella esterna dell’aria circostante il pallone), così come la temperatura (temperatura ambiente). Quindi il volume di un gas è direttamente proporzionale alla sua massa, con una costante di proporzionalità che varia con il tipo di gas.
Però, se invece della massa si usassero il numero di moli, questa costante di proporzionalità risulterebbe essere la stessa in ogni gas e la legge di Boyle diventa la legge dei gas perfetti ovvero:
P⋅V = n⋅R⋅T
In questa formula, la R = 8,314 J/mol K è la costante universale dei gas perché è uguale per ogni gas.
I gas reali non seguono l’equazione di stato di un gas perfetto in modo preciso, specialmente ad alta pressione (alta densità) o quando il gas è vicino alla temperatura di liquefazione. Tuttavia, quando la temperatura è maggiore rispetto a quella di liquefazione e la densità è bassa, la legge dei gas perfetti è utilizzabile anche per i gas reali.
La legge dei gas perfetti è detta equazione di stato dei gas perché mette in correlazione le variabili termodinamiche pressione, volume e temperatura che descrivono lo stato del gas in equilibrio termico.
Quindi, un gas che segue la legge P⋅V = n⋅R⋅T è chiamato gas ideale o perfetto e la T è la temperatura assoluta.
Le leggi di Charles e Gay-Lussac non sono altro che casi particolari della legge dei gas perfetti in cui la pressione o il volume sono costanti.
Sostituendo il numero di moli n nella legge dei gas perfetti con il numero di molecole N diviso il numero di Avogadro NA = 6,023⋅1023 molecole/mole avremmo:
La costante universale dei gas diviso il numero di Avogadro è: k = 1,38⋅10-23 J/K
Se andiamo a sostituire k nella formula finale avremmo: P⋅V = N⋅k⋅T
Da questa formula si può capire come Avogadro intuì che ogni mole di gas ha lo stesso numero di molecole, ma allora non fu in grado di determinare il numero con precisione. Egli ipotizzò che volumi uguali di gas diversi alla stessa pressione e temperatura, contenessero lo stesso numero di molecole.
Questa sua ipotesi è coerente col fatto che la costante universale dei gas è la stessa per ogni gas. Infatti, dalla legge dei gas perfetti segue che due volumi uguali di gas perfetti alla stessa pressione e temperatura hanno un numero di moli n1 e n2:
in cui n1 = n2 solamente se la costante dei gas perfetti R è universale. Inoltre se i due numeri di moli sono uguali, per definizione di mole, i due gas hanno anche lo stesso numero di molecole.
Quindi l’ipotesi di Avogadro è equivalente al fatto che R sia la stessa per tutti i gas.