L’equazione di Nernst definisce la condizione di equilibrio di uno ione fra due soluzioni. Ogni ione in soluzione ha il proprio potenziale dato dall’equazione di Nernst.
Per determinare l’equazione di Nernst bisogna considerare prima il potenziale chimico di una soluzione diluita con concentrazione C contenente una mole di un certo tipo di particelle μ = µ0 + RT lnC dove µ0 è il potenziale chimico standard.
Se le particelle sono costituite da ioni con valenza Z, alla formula precedentemente descritta bisogna aggiungere l’energia potenziale degli ioni dovuta alla presenza di un potenziale elettrico V. Quindi la formula diventa μ = µ0 + RT lnC + ZN0eV. Dove N0 è il numero di Avogadro ed e è la carica elementare. Questa somma viene definita Energia Potenziale Elettrochimica.
Per raggiungere l’equilibrio elettrochimico in una membrana permeabile, si deve avere che la somma dell’energie potenziali elettrochimiche nelle due soluzioni separate da membrana siano uguali e quindi μ1 = μ2. Ciò significa che RT lnC1 + ZN0eV1 = RT lnC2 + ZN0eV2.
Spostando i termini: RT lnC1 – RT lnC2 = ZN0eV1 – ZN0eV2
Facendo il raccoglimento si ottiene:
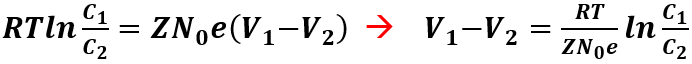
Essendo N0e = F (costante di Faraday), l’equazione diventa:
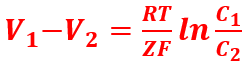
L’equazione di Nernst permette quindi di determinare la differenza di potenziale ai capi di una membrana permeabile quando è in equilibrio elettrochimico. Il potenziale dipende soprattutto dal rapporto fra le concentrazioni degli ioni. Se il potenziale ai due capi della membrana è uguale, allora anche la concentrazione sarà uguale, condizione di equilibrio prevista dalla I legge di Fick per la diffusione libera. Se nel primo compartimento il potenziale è maggiore, significa che nel secondo compartimento c’è una maggiore concentrazione dello ione e viceversa.
L’equilibrio fra i due comparti è quindi possibile solamente se il processo di diffusione dovuto al gradiente di concentrazione (JDsM) ha verso opposto al flusso di soluto determinato dal campo elettrico (JEsM) che è sempre diretto dal potenziale maggiore al potenziale minore.
In condizioni di equilibrio dinamico deve essere: JsM (totale) = JEsM + JDsM = 0
Fonte: Fisica biomedica.


