Una membrana elastica tesa sviluppa delle forze di reazione che sono dirette parallelamente alla superficie della membrana e sono applicate perpendicolarmente ai bordi della membrana stessa.
Si definisce Tensione Elastica τ di una membrana la forza elastica Fel per unità di lunghezza applicata al contorno della membrana. Questa definizione è simile a quella di Tensione Superficiale γ di una lamina di liquido.
La differenza tra τ e γ è che la tensione elastica τ di una membrana dipende dalla sua superficie (numero di molecole costante in superficie), mentre la tensione superficiale γ di una lamina liquida non dipende dalla sua superficie.
Legge di Laplace
La legge di Laplace esprime la relazione fra la tensione superficiale γ di una bolla liquida (es. bolla di sapone) o la tensione elastica τ di una membrana e la differenza di pressione Δp fra la superficie interna e quella esterna della bolla o della membrana.
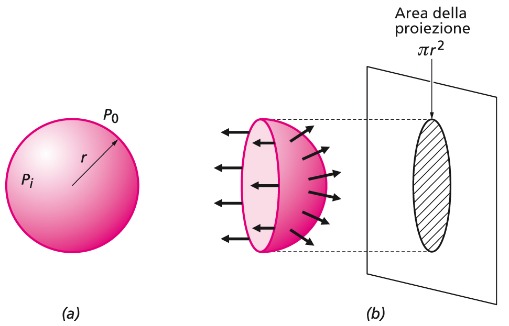
Considerando una membrana sferica di raggio r riempita di un fluido (es. acqua) con differenza tra pressione interna pi ed esterna po uaguale a Δp = pi – po tagliata in 2 parti da un piano verticale, la forza totale Fel esercitata dalla tensione elastica τ dell’emisfero di sinistra su quello di destra è: Fel = τ 2π r
Questa Fel è diretta verso sinistra ed è uguale ed opposta alla risultante Fp delle forze di pressione che agiscono sulla superficie dell’emisfero destro. Tali forze di pressione sono in ogni punto perpendicolari alla superficie sferica.
Le componenti verticali delle Fp di pressione si annullano e la risultante Fp di queste forze è orizzontale e diretta verso destra: Fp = Δp S = Δp π r2
dove S è la proiezione dell’emisfero sul piano verticale. All’equilibrio si ha che la somma delle forze è nulla perciò: Fp + Fel = 0 che sostituendo diventa: Δp π r2 = τ 2π r. Con le opportune semplificazioni e spostamenti dei termini si ha la lege di Laplace per una membrana sferica:
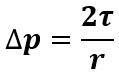
Nel caso di una goccia sferica di liquido si ha:
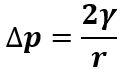
Da questa legge si può osservare come la Δp è proporzionale a (1/r), quindi per conservare la forma di una piccola sfera è richiesta una Δp maggiore di quella necessaria per una sfera grande in condizioni di equilibrio.
Quando si passa dall’esterno all’interno di una bolla sferica (es. bolla di sapone) e non di una goccia, si attraversano due superfici sferiche. Ciascuna di esse è sede di una forza di tensione superficiale γ. Ciò implica un altro fattore 2 nella legge di Laplace: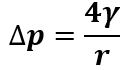
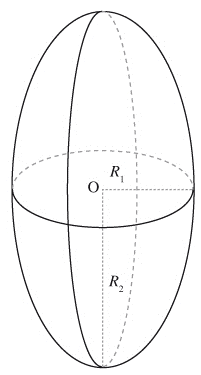
Quando la forma della membrana o della bolla non è sferica ma è ad esempio un ellissoide di rotazione con una certa simmetria, la legge di Laplace più generale, considerando i semiassi R1 e R2 dell’ellissoide è:
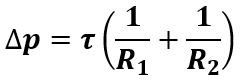
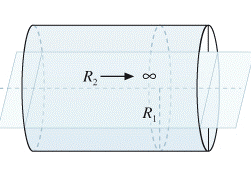
Quando invece la forma della membrana è cilidrica, si può applicare la formula generale individuata prima considerando R2 come lunghezza del cilidro. Nel caso di condotti cilindrici con lunghezza che tende all’infinito R2→∞ e raggio R1, la formula diventa:
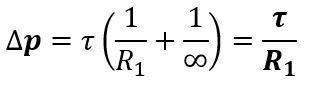
Questa formula, in particolare, è applicabile allo studio dei vasi sanguigni.
In conclusione possiamo dire che la formula di Laplace vale sia per membrane solide elastiche, che per superfici liquide non elastiche. In tal caso la tensione elastica τ è sostituita dalla tensione superficiale γ del liquido che ha valore costante a temperatura costante.
Fonte: Fisica biomedica.