Per comprendere il movimento degli elettroni attorno al nucleo, è utile iniziare con il modello atomico di Rutherford. In questo modello, si assume che gli elettroni si muovano su orbite ellittiche intorno al nucleo, simile al movimento dei pianeti intorno al Sole. Se trascuriamo l’ellitticità delle orbite, il moto di ciascun elettrone può essere approssimato come un moto circolare uniforme. In questo caso, la forza centripeta è rappresentata dalla forza di Coulomb, ovvero dalla forza elettrostatica attrattiva tra il nucleo e l’elettrone.
Per un dato raggio r dell’orbita, l’energia potenziale di un elettrone in un atomo con numero atomico Z è definita come:
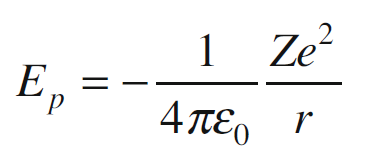
Il segno negativo indica che l’elettrone è attratto dal nucleo. Secondo questa equazione, l’energia potenziale (che è negativa) dell’elettrone aumenta all’aumentare di r, fino ad annullarsi quando la sua distanza dal nucleo diventa molto grande rispetto alle dimensioni dell’atomo.
Ora, supponiamo di voler “estrarre” un elettrone dall’atomo, cioè di spostarlo da una distanza iniziale r dal nucleo (dove l’energia potenziale è uguale a Ep) ad una distanza finale molto grande, praticamente all’infinito (dove l’energia potenziale è nulla). Inoltre, supponiamo che l’energia cinetica dell’elettrone sia la stessa in entrambe le posizioni, iniziale e finale. In tal caso, l’energia necessaria per estrarre l’elettrone è pari al valore assoluto di Ep:
Efinale − Einiziale = 0 − Ep = −Ep
Pertanto, per rimuovere un elettrone dall’atomo, ovvero per ionizzare l’atomo, è necessario fornire un’energia uguale al valore assoluto di Ep. Questa energia è chiamata energia di legame dell’elettrone.
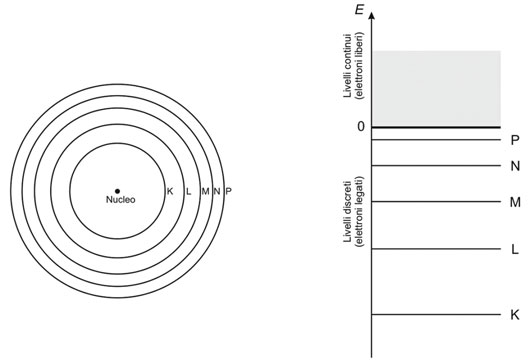
A destra: livelli energetici degli elettroni legati all’atomo (E <0) e liberi (E ≥0).
FONTE: Fondamenti di medicina nucleare. Tecniche e applicazioni.
Tuttavia, il modello atomico di Rutherford è di natura classica e non può spiegare numerosi fenomeni che richiedono un approccio quantistico. All’inizio del Novecento, è stato sostituito dal modello semi-classico di Bohr, che a sua volta è stato perfezionato dalla meccanica quantistica moderna. Nell’attuale modello atomico, ogni elettrone si trova in uno stato quantico specifico, caratterizzato da un preciso valore di energia e altre grandezze fisiche come il momento angolare e lo spin. Queste energie non possono assumere valori continui, ma solo valori discreti o “quantizzati”. Questi valori di energia sono noti come livelli energetici, identificati univocamente dal numero quantico principale n. L’energia degli elettroni in ogni livello aumenta con l’aumentare di n (vedi immagine accanto). Per motivi storici, questi livelli energetici con n = 1, 2, 3, 4, 5 vengono etichettati come K, L, M, N, P.
Per ciascun valore di n, gli elettroni possono assumere diversi valori del numero quantico orbitale l:
l = 0, 1, …, n – 1.
Inoltre, per ogni valore di l, ci sono (2l+1) possibili valori del numero quantico magnetico m. Infine, per ogni valore di m, gli elettroni possono avere due diversi stati di spin.
Di conseguenza, per ciascun valore di l, il numero massimo di elettroni, indicato come Ne, è dato da:
Ne, l = 2(2l+1)
Combinando le equazioni e utilizzando la formula per la somma dei primi k numeri interi che è uguale a k(k+1)/2, otteniamo che il massimo numero di elettroni in un dato livello energetico n è dato da:
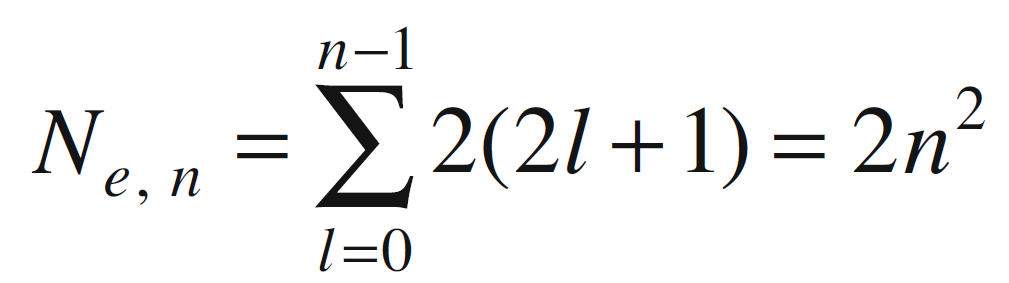
Quindi:
- Ne = 2 per gli orbitali di tipo K;
- Ne = 8 per gli orbitali di tipo L;
- Ne = 18 per gli orbitali di tipo M;
- Ne = 32 per gli orbitali di tipo N;
- Ne = 50 per gli orbitali di tipo P.
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.

