Le radiazioni ionizzanti hanno la capacità di provocare la ionizzazione, ossia l’espulsione di elettroni, negli atomi del materiale attraversato. È possibile distinguere i vari tipi di radiazioni ionizzanti in due categorie principali:
- Radiazioni Corpuscolari: Queste sono costituite da particelle subatomiche cariche, come particelle alfa (α), particelle beta (β), protoni e ioni, nonché da particelle neutre come i neutroni. Queste particelle si muovono ad elevate energie cinetiche.
- Radiazioni Elettromagnetiche: Queste radiazioni comprendono i fotoni X e γ, che sono prive sia di massa che di carica elettrica e si propagano alla velocità della luce.
Una suddivisione ulteriore può essere applicata in base alle interazioni delle radiazioni con la materia. In questo contesto, possiamo distinguere vari tipi di radiazioni in:
- Radiazioni Direttamente Ionizzanti: Queste sono costituite da particelle cariche, come elettroni, protoni, particelle alfa e ioni, che interagiscono direttamente con gli atomi del materiale attraversato. La loro energia cinetica è sufficiente per provocare la ionizzazione mediante collisione con gli elettroni atomici.
- Radiazioni Indirettamente Ionizzanti: Queste radiazioni comprendono particelle prive di carica elettrica, come i neutroni, e fotoni. Quando interagiscono con la materia, possono innescare la ionizzazione indiretta inducendo movimenti di particelle direttamente ionizzanti o causando reazioni nucleari.
I fotoni X e γ possono interagire con gli atomi della materia attraversata attraverso diversi meccanismi, la cui probabilità di occorrenza (sezione d’urto) dipende dall’energia dei fotoni e dal tipo di materiale attraversato. I principali meccanismi di interazione per queste radiazioni sono l’effetto fotoelettrico, l’effetto Compton, e la produzione di coppie.
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.
Effetto fotoelettrico
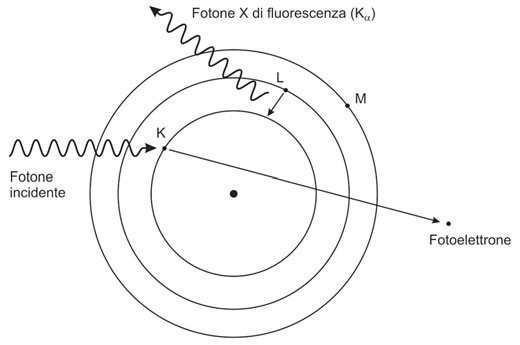
L’effetto fotoelettrico è un fenomeno in cui un fotone interagisce con un elettrone atomico, causando l’espulsione di quest’ultimo dall’atomo. Perché questo fenomeno si verifichi, l’energia del fotone deve essere maggiore dell’energia di legame dell’elettrone coinvolto nell’interazione, tipicamente un elettrone interno come quelli degli orbitali K o L. Dopo la collisione, il fotone scompare e tutta la sua energia viene trasferita all’elettrone espulso. L’energia cinetica finale dell’elettrone (Ke-) è data da:
Ke- = hν – El
Dove hν rappresenta l’energia del fotone e El è l’energia di legame dell’elettrone nell’atomo.
L’orbitale atomico precedentemente occupato dall’elettrone espulso viene successivamente riempito da un altro elettrone atomico proveniente da un orbitale a energia più elevata. Questo processo è accompagnato dall’emissione di un fotone X di fluorescenza.
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.
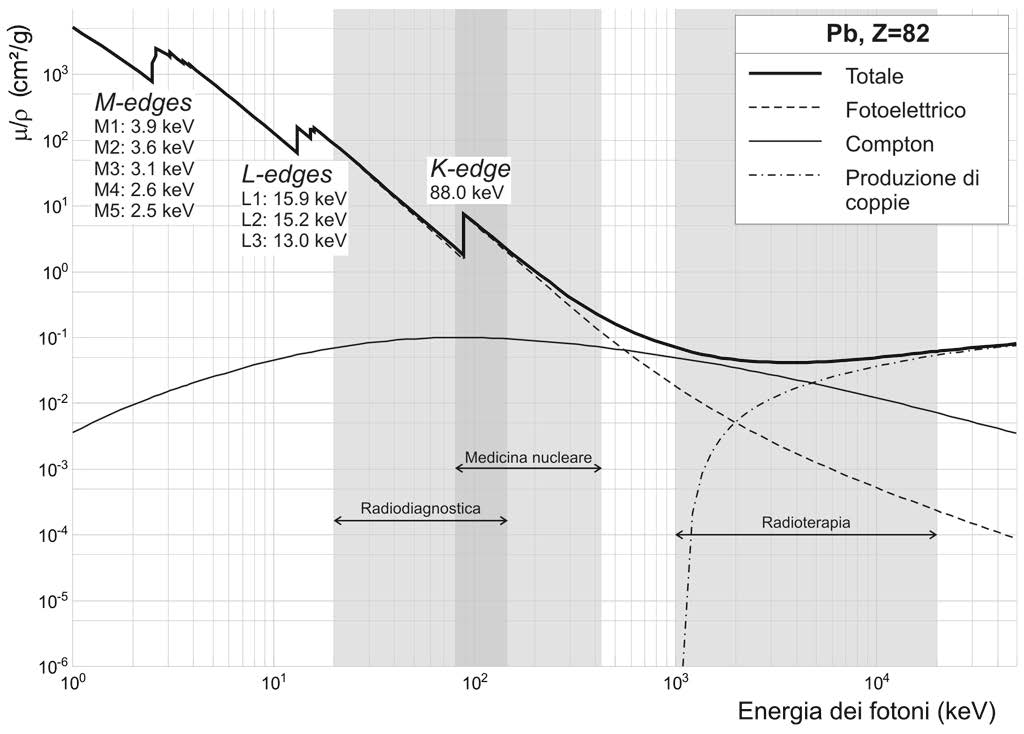
La probabilità che un fotone con un’energia Eγ subisca l’effetto fotoelettrico è proporzionale a Z4/Eγ3, dove Z è il numero atomico del materiale attraversato. Di conseguenza, l’effetto fotoelettrico prevale a basse energie dei fotoni e in materiali con elevato numero atomico. Quando l’energia dei fotoni incidenti varia, la probabilità di subire l’effetto fotoelettrico presenta delle discontinuità, chiamate “edge“. Queste discontinuità si verificano alle energie di legame degli elettroni nei vari orbitali. Ad esempio, il K-edge per un dato materiale si trova all’energia di legame degli elettroni dell’orbitale K. Fotoni con un’energia inferiore al K-edge non possono causare l’effetto fotoelettrico sugli elettroni K poiché non hanno sufficiente energia per espellerli dall’atomo. Lo stesso principio si applica agli L-edges e M-edges.
Effetto Compton
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.
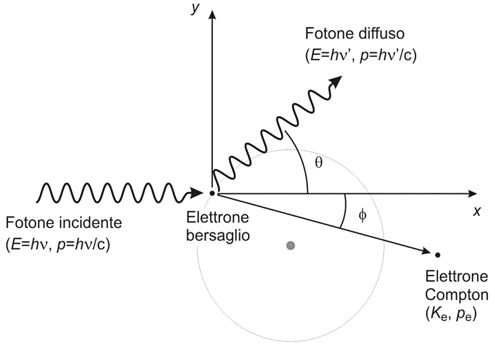
L’effetto Compton è un processo in cui un fotone interagisce con un elettrone atomico. Questa interazione è più rilevante per gli elettroni poco legati all’atomo, come quelli degli orbitali più esterni, poiché si presume che l’energia di legame di questi elettroni sia trascurabile rispetto a quella del fotone incidente. Durante l’interazione, l’elettrone viene espulso dall’atomo, e il fotone viene disperso in una direzione diversa da quella di incidenza. L’energia finale del fotone è minore di quella iniziale perché una parte di essa viene trasferita all’elettrone durante la collisione. L’effetto Compton prevale a energie intermedie e la sua sezione d’urto è approssimativamente proporzionale al numero atomico Z del materiale.
Supponiamo che inizialmente l’energia cinetica e la quantità di moto dell’elettrone siano entrambe nulle, e che la direzione di propagazione del fotone incidente, con energia hν, sia parallela all’asse x. Dopo l’urto, il fotone e l’elettrone sono diffusi a angoli θ e φ rispettivamente. Applicando la conservazione dell’energia e della quantità di moto, otteniamo le seguenti equazioni:
- Conservazione dell’energia: hν + mec2 = hν’ + (mec2 + Ke).
Dove hν’ rappresenta l’energia del fotone dopo l’urto, Ke è l’energia cinetica dell’elettrone dopo l’urto, mec2 è l’energia a riposo dell’elettrone. - Conservazione della quantità di moto lungo l’asse x: hν/c = (hν’/c) cos θ + pe cos φ.
- Conservazione della quantità di moto lungo l’asse y: 0 = (hν’/c) sin θ + pe sin φ.
Nelle equazioni sopra, hν/c rappresenta la quantità di moto del fotone prima dell’urto ed è uguale a hν’/c dopo l’urto. Risolvendo queste equazioni simultaneamente, si può ottenere una relazione tra l’energia iniziale, l’energia finale e l’angolo di diffusione del fotone:
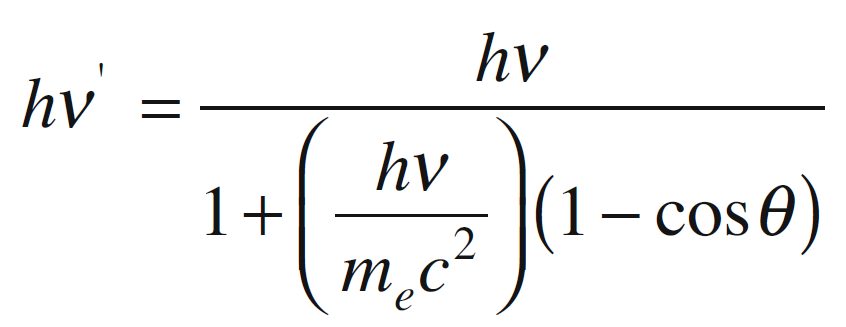
Produzione di Coppie
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.
Nel processo di produzione di coppie, un fotone con energia sufficientemente elevata interagisce con il campo elettrico di un nucleo atomico, “creando” una coppia elettrone-positrone. Questo fenomeno è in accordo con la celebre relazione di Einstein, E = mc2, che stabilisce che l’energia può essere trasformata in materia e viceversa. Dopo la formazione della coppia, il fotone scompare perché tutta la sua energia iniziale è stata trasferita alle particelle create.
Perché questo processo possa verificarsi, l’energia del fotone incidente deve essere maggiore o almeno uguale all’energia a riposo delle due particelle create, cioè dell’elettrone e del positrone:
hν ≥ me−c2 + me+c2 = 2 me−c2 = 1022 keV
La produzione di una coppia elettrone-positrone è quindi un processo a soglia: per energie dei fotoni incidenti inferiori a 1022 keV (chiamata energia di soglia per la produzione di coppie), questo processo non può avvenire perché l’energia disponibile è inferiore alla massa-energia della coppia elettrone-positrone. Nel caso in cui l’energia del fotone sia uguale a quella di soglia, le particelle prodotte avranno energia cinetica e quantità di moto nulle, mentre la quantità di moto del fotone incidente verrà trasferita al nucleo. In questo caso, tutta l’energia disponibile è stata utilizzata per creare l’elettrone e il positrone.
La probabilità di avere produzione di coppie diventa significativa solo a energie molto più elevate della soglia e l’energia in eccesso viene convertita nelle energie cinetiche dell’elettrone e del positrone. Queste energie sono distribuite in modo tale da soddisfare la conservazione dell’energia e della quantità di moto totali durante l’interazione. Per questo motivo, la produzione di coppie non è di interesse in campo radiodiagnostico, dove le energie dei fotoni sono sempre inferiori all’energia di soglia. Tuttavia, la produzione di coppie è il principale meccanismo di interazione, insieme all’effetto Compton, utilizzato in radioterapia, dove i fotoni utilizzati hanno di solito energie comprese tra 1 MeV e 18 MeV.
Coefficiente di Attenuazione Lineare e Legge di Attenuazione Esponenziale
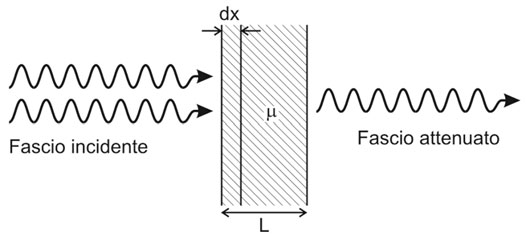
Per descrivere quantitativamente l’interazione di un fascio di raggi X o γ con la materia, si utilizza il coefficiente di attenuazione lineare, indicato con μ. Questo coefficiente rappresenta la probabilità, per unità di spessore, che un fotone interagisca con un atomo attraverso uno dei meccanismi di interazione precedentemente descritti. Il coefficiente di attenuazione lineare ha le dimensioni dell’inverso di una lunghezza e si misura in m-1 nel Sistema Internazionale.
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.
Il coefficiente di attenuazione lineare è una funzione delle sezioni d’urto dei vari processi di interazione dei fotoni con la materia, quindi dipende dall’energia dei fotoni incidenti, dal numero atomico del materiale attraversato e dalla sua densità. Il rapporto tra il coefficiente di attenuazione lineare (μ) e la densità del materiale (ρ) è chiamato coefficiente di attenuazione massico, misurato in m2/kg nel SI.
Per comprendere come il fascio di fotoni diminuisca mentre attraversa un materiale di spessore L, possiamo utilizzare la legge di attenuazione esponenziale. La probabilità che un fotone interagisca con un atomo in uno spessore infinitesimo dx è data da μdx. Dopo aver attraversato questo spessore infinitesimo, il numero di fotoni che non ha subito interazioni diminuisce di una quantità infinitesima, cioè:
dN = -μNdx
Integrando questa equazione su tutto lo spessore L, otteniamo il numero N di fotoni che hanno attraversato l’intero spessore senza subire alcuna interazione:
N = N0e-μL
Questa equazione è conosciuta come la legge di attenuazione esponenziale. È utilizzata per calcolare lo spessore di materiale necessario per attenuare un fascio incidente di una quantità desiderata. Ad esempio, per ridurre l’intensità di un fascio di fotoni monoenergetici di un fattore T = N/N0 = 10-5, lo spessore L necessario può essere calcolato risolvendo:
T = N/N0 = e-μL = 10-5
Risolvendo per L:
ln (e-μL) = ln (10-5)
–μL = –5ln10
L = (5ln10 / μ) ≈ 11,5 / μ
È importante notare che questo calcolo è valido solo per fotoni monoenergetici. In casi in cui il fascio di fotoni ha una distribuzione energetica più complessa, come quelli prodotti dai tubi a raggi X, questo calcolo è valido solo in modo approssimativo, poiché non tiene conto della dipendenza del coefficiente di attenuazione dall’energia.
In radioprotezione, sono comunemente utilizzati lo spessore emivalente (SEV), che è lo spessore necessario per dimezzare il numero di fotoni del fascio incidente, e lo spessore decivalente (SDV), che è lo spessore necessario per ridurre l’intensità del fascio primario di un fattore 10.
Interazioni delle Particelle Cariche con la Materia
Nel paragrafo precedente abbiamo esaminato come i fotoni, privi di carica elettrica, interagiscono con la materia. In seguito a queste interazioni, vengono sempre prodotti elettroni secondari che, a loro volta, interagiscono con gli atomi circostanti, causando ionizzazione. La quantità di ionizzazione prodotta nella materia da un fascio di raggi X o γ è principalmente dovuta alle interazioni degli elettroni secondari. Pertanto, la comprensione dei meccanismi di interazione delle particelle cariche con la materia è importante non solo quando il fascio primario è costituito da particelle α, β o ioni.
A differenza delle particelle neutre, tutte le particelle cariche sono influenzate dal campo elettrico generato dagli elettroni e dai nuclei degli atomi presenti nella materia attraversata. Di conseguenza, è impossibile che attraversino qualsiasi spessore di materiale, per quanto sottile, senza subire interazioni di tipo elettrostatico (o coulombiane). Ogni volta che avviene un urto, le particelle cariche del fascio di radiazione producono eccitazione e ionizzazione nella materia, riducendo progressivamente la loro energia fino a fermarsi. L’energia media persa dalle particelle del fascio per unità di lunghezza è chiamata potere frenante del mezzo e viene indicata con la lettera S:
S = -dE/dx
Il potere frenante dipende in modo complesso dal tipo di particella, dalla sua velocità e dal tipo di materiale attraversato. Nel caso di particelle cariche pesanti come protoni, α e ioni, il potere frenante è approssimativamente dato da:
S ∝ NZz2/v2
Dove Z è il numero atomico del materiale, N è il numero di atomi per unità di volume, v è la velocità della particella e z il suo numero atomico.
Per particelle leggere come elettroni e positroni, il potere frenante è approssimativamente dato da:
S ∝ NZ/v2
Il concetto di “range” è definito come lo spessore medio di materiale attraverso cui una particella carica deve passare affinché essa perda tutta la sua energia cinetica. Il range, indicato con R, è un parametro importante per queste particelle. Tuttavia, va notato che il concetto di range non è applicabile alle particelle neutre, come i fotoni, poiché la loro intensità non può essere ridotta a zero senza attraversare uno spessore infinito di materiale, come previsto dall’Equazione (N = N0e-μL).
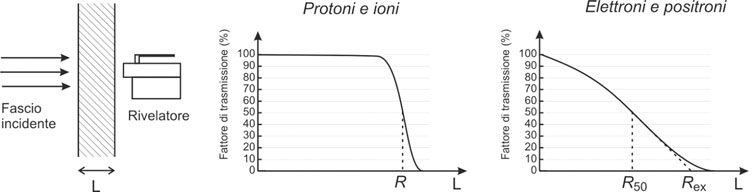
Nel caso di particelle leggere (a destra), il range R50 è definito come lo spessore per cui il fattore di trasmissione è uguale al 50%, mentre il range estrapolato Rex è definito come lo spessore ottenuto proiettando sull’asse delle ascisse la retta tangente alla curva di trasmissione nel punto L=R50.
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.
Le particelle cariche possono perdere energia in vari modi, e uno di essi è la collisione coulombiana anelastica, in cui emettono radiazione elettromagnetica (raggi X) chiamata radiazione di frenamento o bremsstrahlung. Questa radiazione è responsabile di una parte delle perdite di energia delle particelle cariche e le perdite per irraggiamento sono relativamente minori rispetto alle perdite per collisione, particolarmente per particelle cariche pesanti come protoni e ioni. Le perdite per irraggiamento diventano più significative per particelle leggere come gli elettroni. Inoltre, il rapporto tra perdite per irraggiamento e per collisione aumenta con l’aumentare del numero atomico del materiale attraversato. Pertanto, nella progettazione di apparecchiature come tubi radiogeni, in cui la radiazione di frenamento è la principale componente di emissione, si utilizzano materiali ad alto numero atomico come il tungsteno o il molibdeno. D’altro canto, quando si vuole schermare un fascio di elettroni minimizzando l’emissione di radiazione di frenamento, si utilizzano materiali a basso numero atomico come il polietilene o altre plastiche.
Fonte: Fondamenti di medicina nucleare. Tecniche e applicazioni.