La Fisica è una scienza sperimentale che si propone di descrivere i fenomeni naturali attraverso modelli matematici basati sull’osservazione sperimentale. Per farlo, è necessario in primo luogo:
- definire con chiarezza gli “oggetti” che vengono osservati e descritti, ovvero le grandezze fisiche;
- stabilire il metodo di quantificazione di tali oggetti, cioè le operazioni di misura delle grandezze.
Una volta definite le grandezze fisiche e gli enti matematici che ne rappresentano la misura (come numeri, vettori, ecc.), le leggi della Fisica si esprimono come relazioni tra grandezze, formulate a partire dall’esperienza sperimentale.
A partire da alcune relazioni fondamentali, è possibile eseguire manipolazioni matematiche per dedurne altre, capaci di fare previsioni sul comportamento della materia anche in condizioni molto diverse da quelle iniziali. Tuttavia, anche queste leggi derivate devono essere verificate sperimentalmente, per confermare la validità della descrizione adottata.
Tale processo richiede l’impiego di strumenti matematici di varia complessità. In particolare, nello svolgimento di questo corso si presuppone la conoscenza dei seguenti elementi di base:
- algebra e geometria elementare;
- trigonometria;
- logaritmi;
- studio di semplici funzioni;
- concetti di derivazione e integrazione di una funzione.
Caricamento….
Definizione di una grandezza fisica e sue dimensioni
Una grandezza fisica è una quantità alla quale è possibile assegnare un valore numerico attraverso un’operazione di misura. In altre parole, possiamo definire grandezza fisica qualsiasi quantità che possa essere confrontata con un campione omogeneo, scelto come unità di misura.
Ad esempio, la grandezza fisica lunghezza può essere definita scegliendo un’unità di misura appropriata (ad esempio il metro o il centimetro) e stabilendo le operazioni di confronto necessarie tra la lunghezza da misurare e il campione.
Il risultato della misura sarà un numero che esprime il rapporto tra la grandezza considerata e l’unità di riferimento.
In alcuni casi, il confronto con il campione può avvenire direttamente.
In altri casi, ad esempio per lunghezze molto grandi o molto piccole, è necessario ricorrere a relazioni indirette con altre grandezze (come gli angoli), che vengono invece misurate direttamente.
Riprendendo l’esempio precedente: una volta definita l’unità di lunghezza, si può assumere come unità di area quella del quadrato avente per lato l’unità di lunghezza, e come unità di volume il cubo avente per spigolo la stessa unità. In questo caso, diremo che:
- l’unità di lunghezza è una unità fondamentale;
- l’unità di area e l’unità di volume sono unità derivate.
In particolare, si dice che le dimensioni di una superficie S e di un volume V sono, rispettivamente, quelle di una lunghezza al quadrato e di una lunghezza al cubo. Si può scrivere simbolicamente:
[S]=[L2] e [V]=[L3]
Ogni legge fisica mette in relazione i valori di almeno due grandezze fisiche; ciò permette, scegliendo alcune grandezze come fondamentali, di esprimere le altre in funzione di queste.
Le grandezze fondamentali nella Meccanica
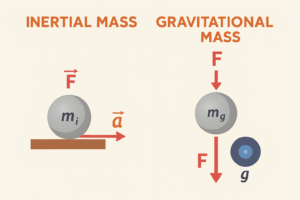
Nel campo della Meccanica si assumono come grandezze fondamentali la massa, la lunghezza e il tempo. Questo significa che tali grandezze non sono definibili in termini di altre: esse rappresentano concetti intuitivi, il cui significato emerge attraverso l’operazione di misura.
Al contrario, tutte le altre grandezze fisiche (come la velocità, l’accelerazione, la forza, il lavoro, la pressione e così via) possono essere definite in termini delle tre grandezze fondamentali.
Per esempio, la velocità è definita come il rapporto tra lo spazio percorso e il tempo impiegato a percorrerlo. Essa è quindi esprimibile come:
[v]=[L][t−1]
Per lo studio di fenomeni non meccanici, è necessario introdurre anche altre grandezze fondamentali. Ad esempio, nello studio dell’elettricità, si introduce la corrente elettrica come quarta grandezza fondamentale.
Sebbene la scelta delle grandezze fondamentali sia, entro certi limiti, arbitraria, in pratica è conveniente considerare fondamentali quelle grandezze la cui definizione operativa è più semplice e la cui comprensione concettuale è più intuitiva.
| Grandezza | S.I. | C.G.S. | Sistemi pratici |
|---|---|---|---|
| GRANDEZZE FONDAMENTALI | |||
| Massa | chilogrammo | grammo | grammomolecola |
| Lunghezza | metro | centimetro | ångström |
| Tempo | secondo | secondo | minuto, ora |
| Corrente elettrica | ampere | – | – |
| GRANDEZZE DERIVATE | |||
| Volume | m³ | cm³ | litro |
| Densità | kg·m⁻³ | g·cm⁻³ | – |
| Forza | kg·m·s⁻² (newton) | g·cm·s⁻² (dyna) | kgpeso |
| Velocità | m·s⁻¹ | cm·s⁻¹ | mm·s⁻¹, km/h |
| Pressione | N·m⁻² (pascal) | dyna·cm⁻² (baria) | atmosfera, mmHg, cmH₂O |
| Lavoro, energia, calore | kg·m²·s⁻² (joule) | g·cm²·s⁻² (erg) | caloria, Caloria |
| Carica elettrica | s·ampere (coulomb) | u.e.s. | – |
Caricamento….
Equazioni dimensionali
Data una generica grandezza fisica X, la sua equazione dimensionale può essere espressa nel modo seguente:
[X]=[Ma][Lb][Tc][Id]
dove:
- M, L, T, I rappresentano rispettivamente massa, lunghezza, tempo e corrente elettrica (le grandezze fondamentali);
- a, b, c, d sono esponenti numerici (positivi, negativi o nulli) che indicano in quale modo la grandezza derivata X dipende dalle grandezze fondamentali.
L’utilità delle equazioni dimensionali risiede nel fatto che ogni legge fisica deve essere dimensionalmente omogenea: cioè tutti i termini di un’equazione devono avere le stesse dimensioni.
In altre parole, solo grandezze fisiche con le stesse dimensioni possono essere sommate o eguagliate.
Il controllo dimensionale è spesso usato per verificare se una relazione fisica è corretta o meno.
Fonte: Fisica biomedica.