La massa è una proprietà fondamentale e intrinseca di un corpo. Essa ne quantifica la materia e, per sua natura, non varia in base alla posizione del corpo nello spazio o nel tempo. Sebbene il concetto sia intuitivo, in fisica si articola in due definizioni operative distinte: la massa inerziale e la massa gravitazionale. La loro perfetta equivalenza, verificata sperimentalmente con estrema precisione, rappresenta uno dei pilastri della fisica moderna.
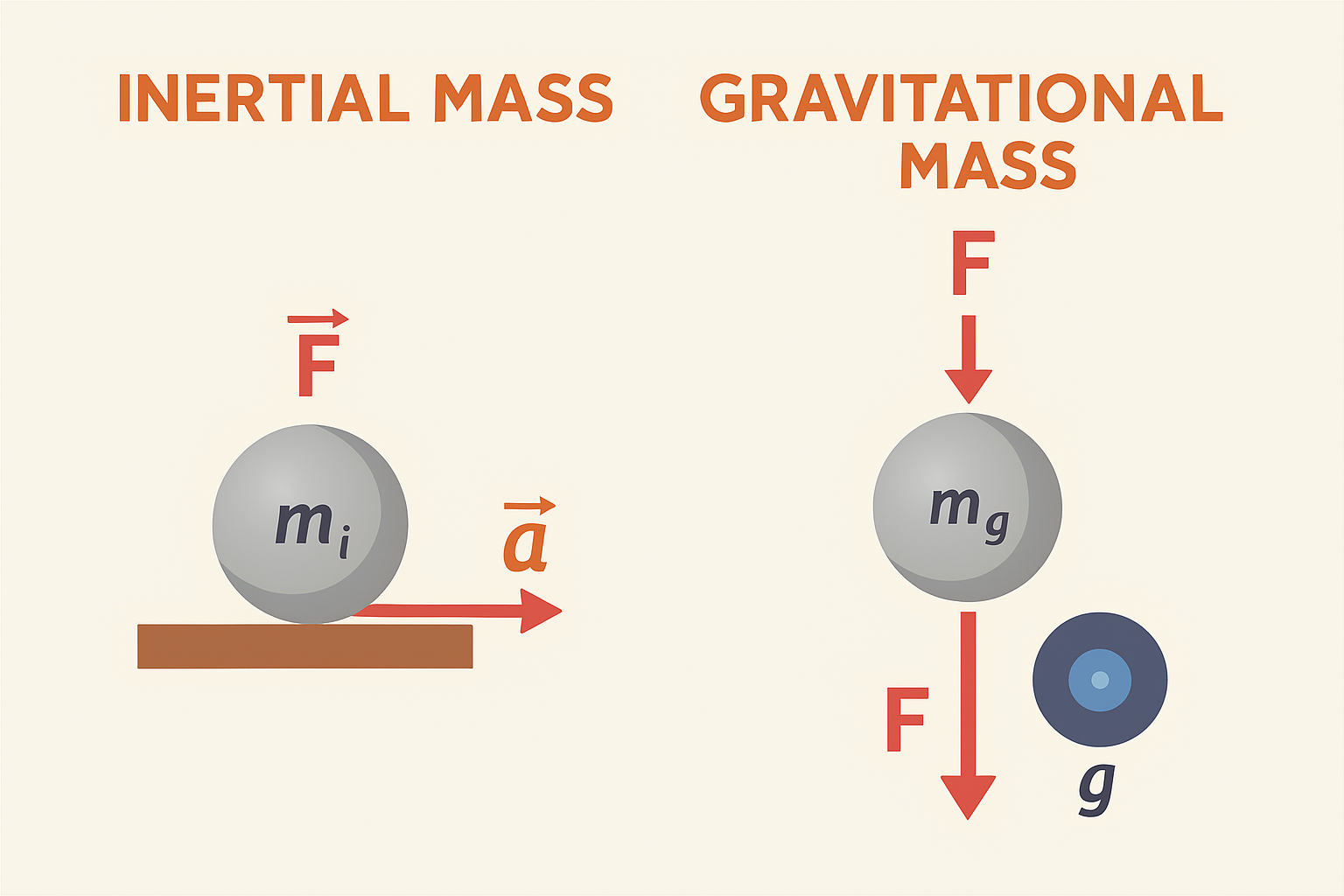
La massa inerziale (mᵢ) è la misura della resistenza che un corpo oppone a un’accelerazione quando viene sottoposto a una forza. Questa definizione discende direttamente dal Secondo Principio della Dinamica, formalizzato dalla relazione fondamentale:
F = mᵢa
In questo contesto, la massa è il coefficiente di proporzionalità che lega la forza applicata (F) all’accelerazione prodotta (a), quantificando l’inerzia del corpo.
La massa gravitazionale (mg) è la proprietà della materia che le permette di generare un campo gravitazionale o di risentire della forza di gravità prodotta da altri corpi. Questa definizione si basa sulla legge di gravitazione universale di Newton. A priori, non sussiste alcun vincolo teorico che imponga l’identità di questa proprietà con la massa inerziale; essa potrebbe dipendere da altre caratteristiche intrinseche della materia, come la sua composizione chimica, la forma o altre proprietà non considerate dall’inerzia.
Now loading…
Nonostante le due definizioni siano concettualmente diverse, è stato verificato sperimentalmente con straordinaria accuratezza che la massa inerziale e la massa gravitazionale sono equivalenti.
mᵢ = mg
Questa equivalenza è stata determinata con una precisione dell’ordine di una parte su 10¹⁸. In virtù di questa fondamentale scoperta, nella pratica comune si farà riferimento a un’unica grandezza fisica, la massa, indicata semplicemente con il simbolo m. Questa equivalenza, apparentemente una coincidenza in meccanica classica, diventerà il postulato fondante della Teoria della Relatività Generale di Einstein.
Stabilita la natura intrinseca della massa, è ora fondamentale distinguerla nettamente dalla sua manifestazione più comune nel campo gravitazionale terrestre: il peso.
La forza peso
A differenza della massa, il peso non è una proprietà intrinseca di un corpo, ma una forza. Nello specifico, il peso è la forza con cui un corpo di massa m viene attratto dalla massa terrestre a causa dell’interazione gravitazionale. Comprendere questa distinzione è cruciale per analizzare correttamente fenomeni fisici che avvengono in contesti in cui la gravità non è costante, come ad esempio a diverse altitudini o su altri corpi celesti.
La relazione matematica fondamentale che lega la massa (m) al peso (P) è un caso particolare del Secondo Principio della Dinamica:
P = mg
In questa formula, l’accelerazione generica a è sostituita dall’accelerazione di gravità g. Poiché il valore di g varia in funzione della posizione (ad esempio, diminuisce con l’aumentare dell’altitudine), il peso di un corpo è una grandezza vettoriale dipendente dalla posizione, a differenza della sua massa, che rimane costante.
Oltre a massa e peso, un’altra grandezza fondamentale per caratterizzare i materiali, specialmente i mezzi continui, è la densità.
La densità
Per descrivere le proprietà di un mezzo continuo, sia esso solido, liquido o gassoso, è spesso più utile e significativo conoscere la sua densità piuttosto che la sua massa totale. La densità è una grandezza intensiva che misura la concentrazione di massa in un determinato volume.
Si distinguono due definizioni principali di densità:
- densità assoluta (d): è definita come il rapporto tra la massa del corpo e il volume che esso occupa:
d=m/V; - densità relativa (dᵣ): è definita come il rapporto tra la massa di un corpo e la massa di un uguale volume di acqua distillata alla temperatura di 4°C (condizione in cui l’acqua ha la sua massima densità). Essendo un rapporto tra due masse, la densità relativa è un numero adimensionale.
Un concetto analogo è quello di peso specifico, definito come il rapporto tra il modulo della forza peso di un corpo e il suo volume. Le definizioni di peso specifico assoluto e relativo seguono la stessa logica di quelle per la densità.
La distinzione concettuale tra queste grandezze è spesso offuscata dall’uso improprio e indifferenziato delle loro unità di misura, un’ambiguità che la prossima sezione si propone di chiarire.
Sistemi di unità di misura e ambiguità comuni
Gran parte della confusione tra massa e peso deriva dall’uso storico e pratico di diversi sistemi di unità di misura. Un’analisi comparata dei sistemi Internazionale (SI), C.G.S. e pratico (o tecnico) permette di evidenziare le corrette attribuzioni delle unità a massa e forza.
| Sistema | Unità di massa | Unità di forza |
|---|---|---|
| Sistema Internazionale (SI) | chilogrammo-massa (kg) – fondamentale | newton (N) – derivata |
| Sistema C.G.S. | grammo-massa (g) – fondamentale | dyna (dyn) – derivata |
| Sistema pratico (o tecnico) | chilogrammo-massa (kgₘ) – derivata | chilogrammo-peso (kgₚ) – fondamentale |
L’origine della confusione risiede nel fatto che nel linguaggio comune e in alcuni ambiti tecnici, il termine “chilogrammo” viene usato per indicare il peso. Come evidenziato dalla tabella, questa pratica deriva dal sistema pratico, oggi largamente in disuso in ambito scientifico. In tale sistema, il chilogrammo-peso (kgₚ) è un’unità di forza, definita come quella forza che imprime a un corpo di massa 1 kg un’accelerazione pari a quella di gravità standard, convenzionalmente 9.8 m/s².
Per esempio, un corpo che nel sistema pratico ha un peso di 10 kgₚ possiede, per definizione, una massa di 10 kgₘ. Per esprimere il suo peso nel Sistema Internazionale, si esegue la conversione: P = mg = (10 kg) * (9.8 m/s²) ≈ 98 N.
Chiarite le distinzioni tra grandezze reali e le loro unità, è ora necessario esplorare un’altra categoria di forze, le forze apparenti, che emergono quando si abbandonano i sistemi di riferimento inerziali.
Le forze apparenti (o pseudoforze)
I principi della dinamica sono validi esclusivamente nei sistemi di riferimento inerziali, ovvero quei sistemi in cui vige il principio d’inerzia (un corpo non soggetto a forze permane nel suo stato di quiete o di moto rettilineo uniforme). Quando si osserva un moto da un sistema di riferimento accelerato (non inerziale), le leggi di Newton non sembrano più valide. Per preservarne la validità formale, è necessario introdurre delle “forze apparenti” o “pseudoforze”.
L’introduzione di queste forze risponde a un’esigenza matematica di preservare la covarianza delle leggi della dinamica nel passaggio a un sistema di riferimento non inerziale. L’equazione del moto per un corpo di massa m, osservato da un sistema non inerziale, assume la forma F - mac = marel, dove F sono le forze reali, ac l’accelerazione del sistema e arel l’accelerazione del corpo relativa al sistema. Per ripristinare la forma canonica Ftotale = marel, si sposta il termine -mac al primo membro, definendolo come forza apparente F':
F' = -mac
Questa forza ha sempre verso opposto a quello dell’accelerazione del sistema di riferimento.
Esempi di forze apparenti:
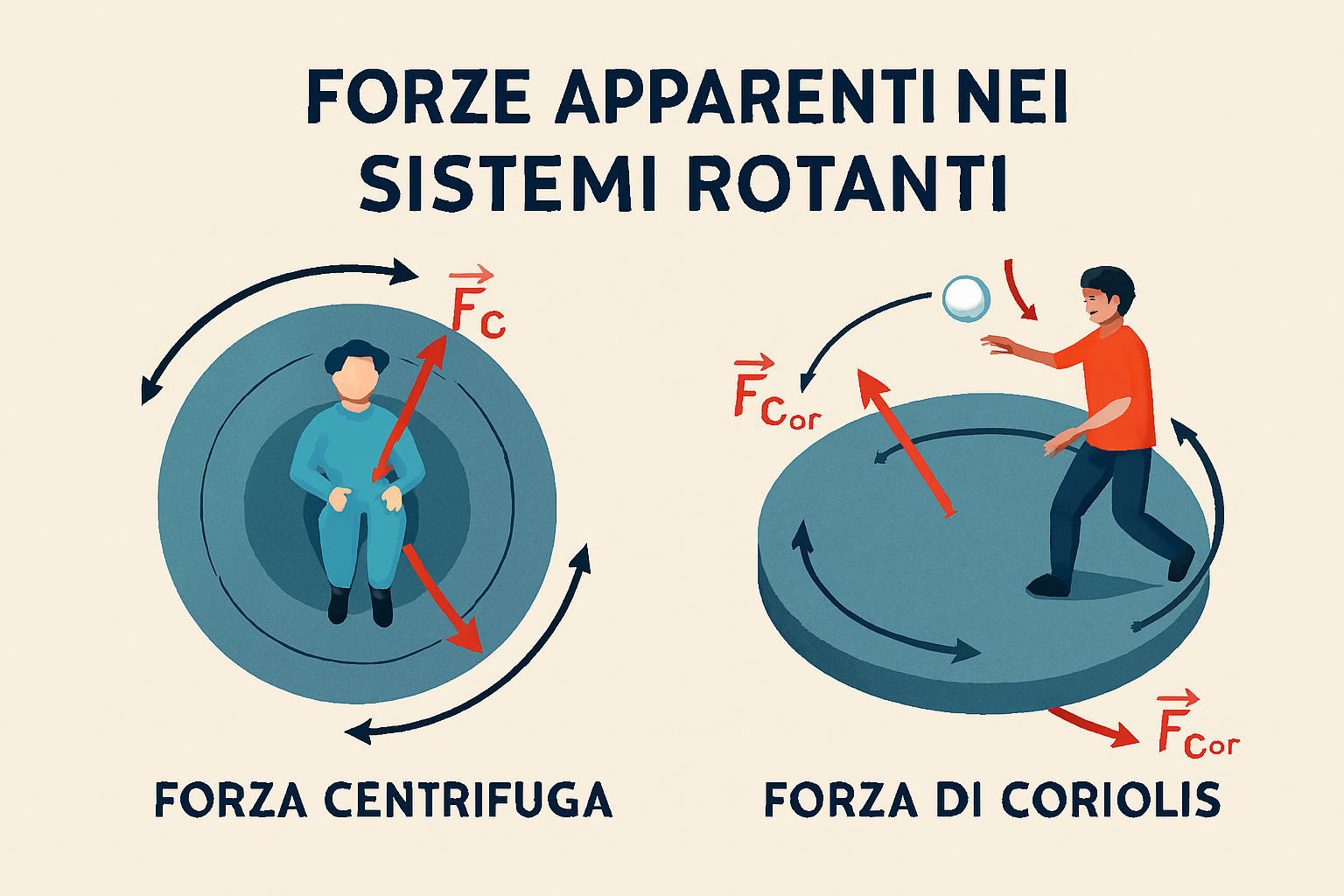
- forza centrifuga: è una forza apparente che si manifesta in un sistema di riferimento in moto circolare. Nasce per compensare l’accelerazione centripeta necessaria a mantenere un corpo in traiettoria curva e viene percepita da un osservatore solidale con il sistema rotante come una forza che spinge i corpi verso l’esterno;
- forza di Coriolis: è un’altra forza apparente presente nei sistemi in rotazione. Si manifesta quando un corpo si muove con una certa velocità rispetto al sistema rotante. Ad esempio, una palla lanciata in linea retta su una piattaforma girevole apparirà, a un osservatore sulla piattaforma, deviare trasversalmente alla direzione del moto, seguendo una traiettoria curva a causa di questa forza.
La Forza di Coriolis ha implicazioni pratiche di enorme importanza, giocando un ruolo fondamentale nella dinamica atmosferica e nella meteorologia. È infatti responsabile dell’influenza sui venti, sulla formazione e il senso di rotazione di cicloni e uragani, e sulla direzione delle principali correnti oceaniche.
È opportuno notare che la distinzione tra forze “reali” e “apparenti” è, in una certa misura, arbitraria, poiché si basa sull’assunto che esista un sistema di riferimento inerziale assoluto nell’universo in cui le forze osservate sono tutte “reali”.
Fonte: Fisica biomedica.