La matematica rappresenta il linguaggio fondamentale attraverso cui le scienze fisiche descrivono, interpretano e prevedono i fenomeni naturali. I concetti sviluppati nell’ambito della geometria e dell’analisi matematica non sono meri strumenti astratti, ma costituiscono prerequisiti essenziali per la modellizzazione rigorosa e quantitativa dei processi fisici. Questa necessità è particolarmente sentita nei campi applicativi moderni, come il settore medico-biologico, dove la precisione descrittiva è cruciale per comprendere meccanismi complessi, dalla propagazione dei segnali bioelettrici all’assorbimento di radiazioni nei tessuti.
Per costruire questa comprensione, è indispensabile partire dalle fondamenta: la descrizione geometrica dello spazio in cui i fenomeni hanno luogo.
Fondamenti di geometria
La geometria fornisce il quadro concettuale e quantitativo per descrivere lo spazio fisico. La comprensione delle forme, delle loro dimensioni e delle loro proprietà intrinseche è il primo passo indispensabile per definire il “palcoscenico” su cui si svolgono i fenomeni fisici e per misurare correttamente le grandezze spaziali.
Formule geometriche essenziali
Le proprietà di base delle figure piane e solide sono ricorrenti nell’analisi di sistemi fisici. La tabella seguente riassume le formule più importanti per il calcolo di aree, volumi e perimetri.
| Forma geometrica | Formula rilevante |
|---|---|
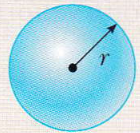 Sfera | Superficie: 4πr²Volume: (4/3)πr³ |
 Cilindro | Superficie laterale: 2πrlVolume: πr²l |
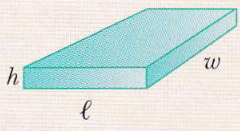 Parallelepipedo | Superficie: 2(lh + lw + hw)Volume: lwh |
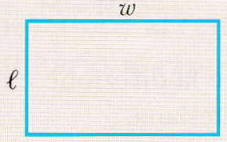 Rettangolo | Area: lwPerimetro: 2(l + w) |
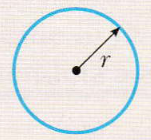 Cerchio | Area: πr²Circonferenza: 2πr |
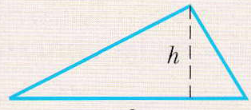 Triangolo | Area: (1/2)bh |
L’angolo piano e l’angolo solido
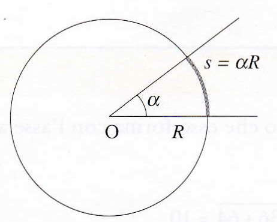
In questo modo l’angolo a viene misurato in radianti.
L’angolo piano è un concetto bidimensionale definito come il rapporto tra la lunghezza di un arco di circonferenza e il raggio della circonferenza stessa. Le sue unità di misura principali sono i gradi sessagesimali (360° per un angolo giro) e i radianti (2π radianti per un angolo giro).
L’angolo solido rappresenta l’estensione tridimensionale del concetto di angolo piano. È definito come il rapporto tra l’area di una porzione di superficie sferica (una “calotta”) e il quadrato del raggio della sfera. Questo concetto, apparentemente astratto, assume un’importanza cruciale in numerose applicazioni medico-biologiche, tra cui:
- l’interpretazione dei segnali elettrocardiografici;
- la modellizzazione della propagazione e della rivelazione di onde sonore;
- la descrizione della propagazione di onde elettromagnetiche e radiazioni corpuscolari.
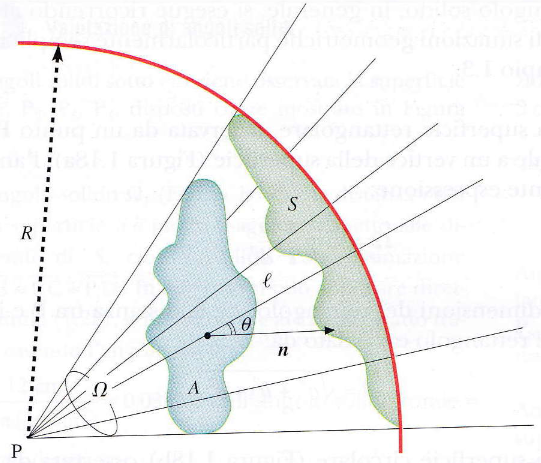
L’angolo solido (Ω) viene misurato in steradianti (sr) secondo la formula:
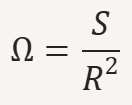
dove S è l’area della calotta sferica e R è il raggio della sfera.
Poiché la superficie totale di una sfera è 4πR², l’angolo solido totale che circonda un punto è 4π steradianti. In alternativa, può essere espresso come frazione dell’angolo solido totale:
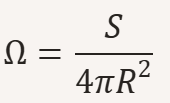
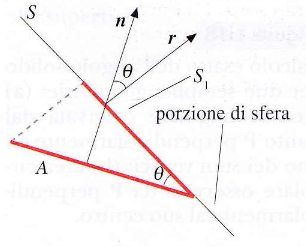
S1= A cosθ = A n ⋅ r
dove n e r sono i versori unitari normali rispettivamente alla superficie A e alla superficie sferica S
1.
Questa forma adimensionale rappresenta la porzione di spazio sferico totale sottesa dalla superficie.
Un aspetto fondamentale dell’angolo solido è la sua dipendenza dall’orientamento della superficie osservata rispetto al punto di osservazione. L’area S proiettata sulla sfera dipende dall’angolo θ tra la normale alla superficie A e la direzione di osservazione. L’area proiettata, e di conseguenza l’angolo solido, è proporzionale al coseno di questo angolo θ.
L’esempio di calcolo che segue illustra efficacemente come l’angolo solido cambi in base alla posizione e all’orientamento reciproci tra osservatore e superficie. I quattro casi analizzati sono:
- caso P1 (osservazione frontale): il punto di osservazione si trova sulla normale alla superficie. L’angolo solido è calcolato direttamente come rapporto tra l’area della superficie
Se4πr², assumendo che la distanzarsia molto maggiore delle dimensioni della superficie; - caso P2 (osservazione angolata): la superficie è osservata con un angolo di 30°. La sua proiezione effettiva è ridotta di un fattore
cos(30°), risultando in un angolo solido inferiore rispetto al caso P1; - caso P3 (osservazione laterale): la superficie è vista di lato (angolo di 90°). La sua proiezione sulla sfera è nulla (
cos(90°) = 0), e di conseguenza l’angolo solido sotteso è zero; - caso P4 (osservazione dal piano della superficie): il punto di osservazione giace sulla superficie stessa. In questa configurazione, la superficie sottende un intero emisfero, corrispondente a un angolo solido di
2πsteradianti, ovvero il 50% dell’angolo solido totale.
È cruciale sottolineare che le formule S/4πr² e S cos(θ)/4πr² utilizzate in questi esempi costituiscono un’approssimazione valida solo quando la distanza di osservazione r è molto maggiore delle dimensioni della superficie S. In molte applicazioni reali, specialmente nell’imaging biologico dove si analizzano sorgenti estese o in prossimità dei rivelatori, questa approssimazione non è applicabile. In tali scenari, il calcolo dell’angolo solido richiede la risoluzione di un calcolo integrale. Per geometrie semplici, come un rettangolo o un cerchio osservati da punti specifici, esistono soluzioni analitiche esatte, a riprova della complessità intrinseca del problema.
Aver definito il quadro statico dello spazio attraverso la geometria ci impone ora un cambio di prospettiva: dobbiamo introdurre gli strumenti per descrivere le relazioni dinamiche tra le grandezze fisiche che operano al suo interno. Questo passaggio ci conduce al concetto di funzione.
Il concetto di funzione
Il concetto di funzione è lo strumento matematico primario per modellare la dipendenza tra grandezze fisiche variabili. Attraverso lo studio di specifiche famiglie di funzioni, è possibile non solo descrivere lo stato di un sistema in un dato istante, ma anche comprendere e prevedere la sua evoluzione.
In una relazione funzionale, si distinguono una variabile indipendente (x), alla quale si possono assegnare valori arbitrari, e una variabile dipendente (y), i cui valori sono determinati da x secondo una regola precisa. Questa relazione si esprime con la notazione: y = f(x) Le funzioni si classificano in:
- monodrome (a un solo valore): ad ogni valore di
xcorrisponde un solo valore diy. Un esempio è la funzione che descrive la popolazione italiana nel tempo; - polidrome (a più valori): ad ogni valore di
xpossono corrispondere più valori diy. Un esempio è la relazioney² = x, dove perx > 0si hanno due soluzioniy = +√xey = -√x.
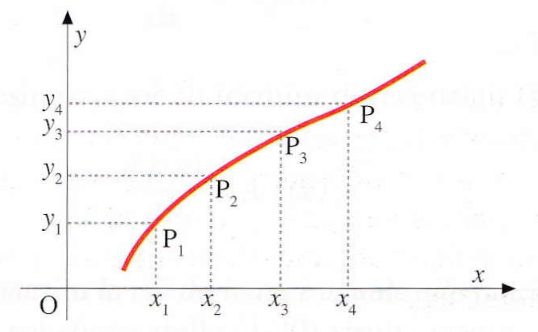
Graficamente, una funzione y = f(x) viene rappresentata su un piano cartesiano, dove ad ogni coppia di valori (x, y) corrisponde un punto. L’insieme di tutti questi punti forma una curva che visualizza l’andamento della funzione.
La funzione lineare
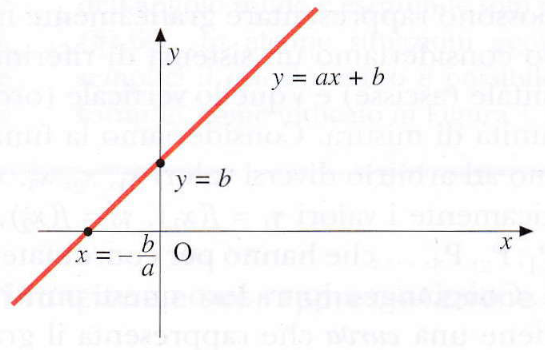
La funzione lineare descrive una relazione di proporzionalità diretta tra due variabili ed è espressa dalla forma generale: y = ax + b.
La sua rappresentazione grafica è una retta, i cui parametri hanno un significato fisico preciso:
aè il coefficiente angolare, che determina l’inclinazione della retta (la pendenza).bè l’intercetta, ovvero il valore diyquandox = 0.
Un’applicazione fisica classica è la descrizione del moto rettilineo uniforme, la cui legge oraria è: x = x₀ + vt.
In questo modello, la posizione x è una funzione lineare del tempo t. Il grafico spazio-tempo è una retta dove la velocità v corrisponde al coefficiente angolare.
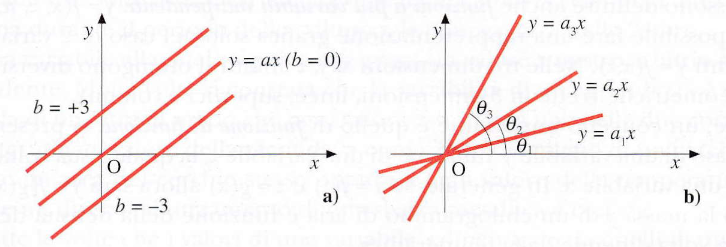
b) la funzione lineare al variare del coefficiente a (coefficiente angolare).
La funzione esponenziale
La funzione esponenziale è fondamentale per descrivere fenomeni in cui la variazione di una grandezza è direttamente proporzionale alla grandezza stessa. Questa proprietà è formalizzata dall’equazione:
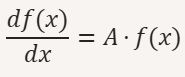
Questa relazione è una fondamentale equazione differenziale lineare del primo ordine, la cui soluzione unica è la funzione esponenziale, evidenziandone la natura primigenia nel descrivere sistemi dove il cambiamento è proporzionale allo stato corrente. La soluzione generale è:
f(x)= h⋅eAx + k
dove h, A e k sono costanti determinate dalle condizioni specifiche del fenomeno. Le sue applicazioni in ambito biofisico sono straordinariamente vaste e includono:
- distribuzione di concentrazione nella centrifugazione;
- carica e scarica del condensatore (fondamentale per il modello della membrana cellulare come circuito RC);
- proprietà di cavo degli assoni nervosi;
- equazioni di Nernst e di Goldman per i potenziali di membrana;
- assorbimento di ultrasuoni, luce, raggi X e raggi gamma nei tessuti;
- decadimento di nuclei radioattivi (alla base di tecniche di imaging come la PET e della radioterapia);
- crescita di colture batteriche.
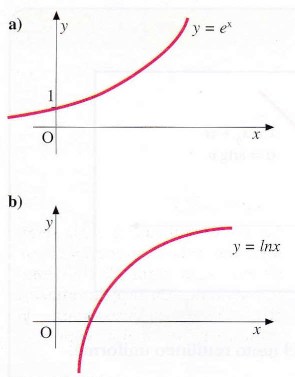
rappresentazione grafica scambiando gli assi.
Ad esempio, nel modellizzare la crescita batterica, l’incremento istantaneo del numero di batteri, dN(t)/dt, è direttamente proporzionale al numero di batteri presenti, N(t). Ciò conduce all’equazione differenziale dN/dt = AN(t), la cui soluzione N(t) = N₀eAt rappresenta il classico modello di crescita esponenziale.
Data la rapida variazione della funzione esponenziale, per la sua rappresentazione grafica si utilizza spesso la carta semilogaritmica. Questo tipo di grafico, avente una scala verticale logaritmica, permette di “linearizzare” una relazione esponenziale del tipo y = A · exp(kx).
Applicando il logaritmo si ottiene:
log(y) = log(A⋅ekx) = log(A) + kx⋅log(e)
Questa espressione corrisponde direttamente all’equazione di una retta Y = b + aX, dove Y = Log(y), l’intercetta b = Log(A), e il coefficiente angolare a = k · Log(e).
Le funzioni trigonometriche
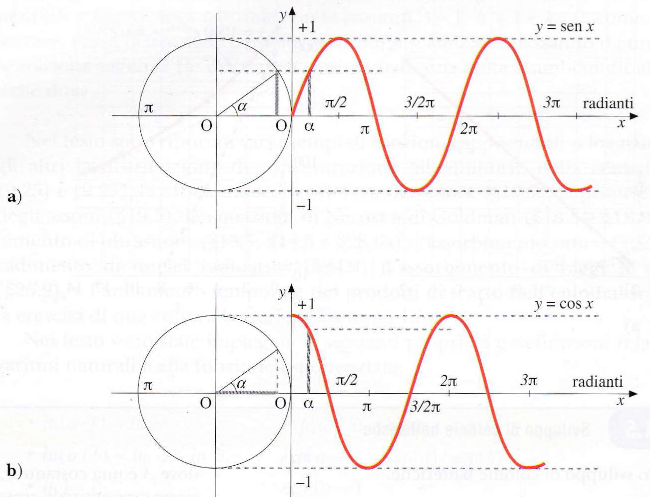
Le funzioni trigonometriche seno, coseno e tangente sono definite a partire dalle proiezioni di un punto che si muove su un cerchio di raggio unitario (il cerchio trigonometrico). Sono caratterizzate da un andamento periodico e oscillatorio. La relazione fondamentale che le lega è:
sen2α + cos2α = 1
Grazie alla loro natura periodica, queste funzioni sono lo strumento matematico essenziale per la descrizione di tutti i fenomeni ondulatori, dal suono alla luce, fino alle onde meccaniche nel corpo umano.
| Gradi (°) | Radianti (rad) | sin α | cos α | tan α |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 |
| 45° | π/4 | √2/2 | √2/2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 |
| 90° | π/2 | 1 | 0 | infinito |
Caricamento….
Strumenti del calcolo infinitesimale
Dopo aver definito le funzioni che descrivono lo stato di un sistema, è necessario introdurre un apparato matematico per analizzare come questo stato cambi nel tempo e nello spazio. Questo ci porta al dominio del calcolo infinitesimale, lo strumento per quantificare il cambiamento.
Il calcolo infinitesimale, con i suoi due concetti cardine di derivata e integrale, fornisce il framework matematico per lo studio del cambiamento. La derivata quantifica i tassi di variazione istantanei, permettendo di analizzare la rapidità con cui un fenomeno evolve, mentre l’integrale consente di accumulare gli effetti di tali variazioni per calcolare quantità totali.
La derivata
La derivata di una funzione y = f(x) in un punto, indicata come dy/dx o f'(x), è definita come il limite del rapporto incrementale per un incremento della variabile indipendente che tende a zero.
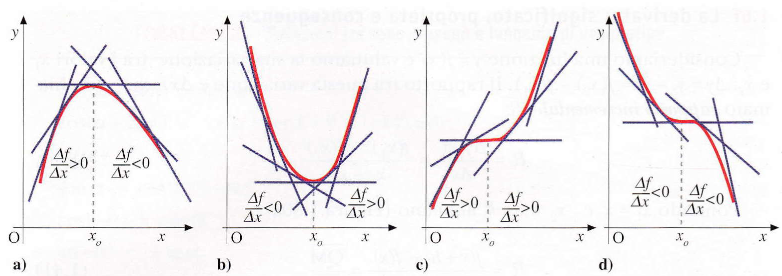
- Interpretazione geometrica: la derivata in un punto
xcorrisponde al coefficiente angolare (tg α) della retta tangente alla curvay = f(x)in quel punto. Essa misura quindi l’inclinazione locale della funzione. - Applicazione pratica: un’applicazione fondamentale delle derivate è la ricerca dei punti di massimo e minimo di una funzione. In questi punti stazionari, la tangente alla curva è orizzontale, il che significa che il suo coefficiente angolare è nullo. Pertanto, i massimi e i minimi si trovano annullando la derivata prima (
f'(x) = 0).
La tabella seguente riporta le derivate di alcune funzioni di uso comune.
Funzione y = f(x) | Derivata dy/dx = f'(x) |
|---|---|
axⁿ | naxⁿ⁻¹ |
ln(x) | 1/x |
eˣ | eˣ |
sen(x) | cos(x) |
cos(x) | -sen(x) |
L’integrale
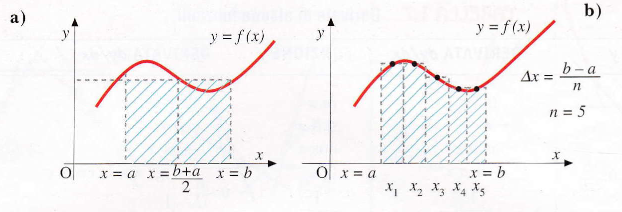
In (a), l’area è valutata su un unico intervallo (b – a).
In (b), la stessa area è stimata suddividendo il dominio in 5 intervalli uguali, per ottenere una stima più precisa.
L’integrale definito, indicato con ∫ₐᵇ f(x)dx, nasce per risolvere il problema del calcolo dell’area sottesa da una curva y = f(x) tra due punti a e b. Concettualmente, esso rappresenta la somma delle aree di un numero infinito di rettangoli con base infinitesima dx e altezza f(x).
L’integrazione e la derivata sono legate da una relazione fondamentale: sono l’una l’operazione inversa dell’altra. Per calcolare un integrale, si cerca una funzione primitiva F(x), ovvero una funzione la cui derivata sia la funzione integranda: F'(x) = f(x).
Caricamento…
L’integrale indefinito, ∫ f(x)dx, rappresenta la famiglia di tutte le primitive di f(x) e si scrive come F(x) + C, dove C è la costante di integrazione, che riflette il fatto che la derivata di una costante è zero.
Un’applicazione fisica che dimostra la potenza di questo strumento è il calcolo del centro di massa. La sua posizione vettoriale rcm è definita dall’integrale rcm = (1/M) ∫ r dm. Per calcolare il centro di massa di un semianello omogeneo di raggio R, si esprime l’elemento di massa dm in termini dell’angolo dθ come dm = λ ds = λ (R dθ), dove λ è la densità lineare di massa. L’integrazione delle posizioni ponderate per la massa lungo la geometria del semianello porta al risultato rcm = (2R/π)uy, localizzando il centro di massa sull’asse di simmetria.
Le equazioni differenziali
La combinazione di funzioni e delle loro derivate in un’unica espressione è ciò che dà origine allo strumento di modellizzazione più potente della fisica: le equazioni differenziali, che traducono le leggi fondamentali della natura in un formato matematicamente risolvibile.
Le equazioni differenziali sono relazioni matematiche che legano una funzione incognita alle sue derivate, permettendo di descrivere non solo lo stato di un sistema, ma le leggi che governano la sua evoluzione dinamica nel tempo e nello spazio.
Un’equazione differenziale è una relazione che contiene una funzione incognita e una o più delle sue derivate. Risolvere un’equazione differenziale significa trovare la funzione che soddisfa tale relazione. Il processo di risoluzione richiede operazioni di integrazione, e la soluzione generale contiene tipicamente delle costanti arbitrarie. Queste costanti vengono determinate imponendo le condizioni al contorno, ovvero valori della funzione o delle sue derivate specificati al contorno del dominio di interesse, dettati dal contesto fisico del problema.
Una delle equazioni differenziali più pervasive è quella che descrive i processi di crescita o decadimento proporzionale:
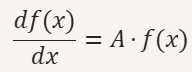
Questa equazione si risolve con il metodo di separazione delle variabili. I passaggi matematici sono i seguenti:
- separare le variabili
f(x)ex: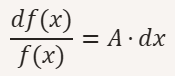
- integrare entrambi i membri dell’equazione:
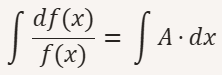
- risolvere gli integrali per ottenere la relazione logaritmica:
ln∣f(x)∣=Ax+C - esprimere
f(x)applicando la funzione esponenziale, che è l’inversa del logaritmo:f(x)= eAx+C = eC⋅eAx = h⋅eAx
doveh=eCè una costante.
Questo procedimento porta direttamente alla soluzione esponenziale, confermando che tale funzione è la descrizione matematica intrinseca dei sistemi in cui il tasso di variazione è proporzionale alla quantità presente.
La potenza dell’approccio basato sulle equazioni differenziali si estende a quasi ogni campo della fisica. Altri esempi rilevanti includono:
- l’equazione del moto armonico: un’equazione differenziale di secondo grado la cui soluzione è una funzione sinusoidale (seno o coseno), che descrive tutti i sistemi oscillanti;
- l’equazione delle onde di d’Alembert: un’equazione alle derivate parziali la cui soluzione descrive la propagazione di qualsiasi fenomeno ondulatorio, dalle onde su una corda alle onde elettromagnetiche.
Le equazioni differenziali rappresentano la sintesi finale e più potente degli strumenti matematici analizzati, capaci di tradurre i principi fisici in modelli predittivi.
Fonte: Fisica biomedica.